کتاب حاضر دربردارنده مباحثی درباره کیهانشناسی و فیزیک نظری است که برای افراد علاقه‌مند، دانش‌آموزان و دانشجویان رشته‌های مرتبط که مایلند درمورد موضوعات مربوطه نوعی بینش مقدماتی را کسب کنند نگاشته شده. در قیاس با بیشتر کتابهایی که در این زمینه منتشر شده‌اند، نویسنده با سبک و سیاق مخصوص به خود سعی کرده مباحث را از زاویای جالبتری مورد بحث قرار دهد، و فروش بالای این کتاب نشان داده که در این کار موفق نیز بوده است. خلیلی بصورت عمدی از کاربرد زبان فنی پرهیز کرده تا شاید آن را برای کسانی که اهل ریاضیات نیستند ساده‌تر و دلپزیرتر کند. ولی خواننده باید توجه داشته باشد که توصیف و تفسیر چنین مباحثی بدون استفاده از ریاضیات (پیشرفته) تقریباً غیر ممکن است و این کتاب تنها می‌تواند مشوقی باشد تا علاقمندان با شور بیشتری مباحث مربوطه را در سطوح بالاتر دنبال کنند. در پایان کتاب فهرستی از مراجع مرتبط با موضوع این کتاب آمده تا درصورت تمایل، خواننده علاقمند بتواند به آنها رجوع کند، که البته تعداد انگشت‌شماری از آنها به زبان فارسی ترجمه شده‌اند.

درباره نویسنده

دکتر جیم الخلیلی فیزیکدان انگلیسی عرب-تبار است که اکنون در دانشگاه سوری انگلستان به تدریس فیزیک کوانتوم مشغول است. او علاوه بر تدریس، به ساختن فیلم‌های مستند علمی نیز اشتغال دارد و سری فیلم‌هایی که بهمراه فیلسوف و ریاضیدان برجسته سِر راجر پِن‌رُز برای شبکه BBC تهیه کرد مورد اقبال زیادی قرار گرفت. خواننده می‌تواند بسیاری از مباحث مطرح شده در این فیلم‌ها را با جزئیات بیشتری در کتاب حاضر پیدا کند.

اضافات مترجم

بعضی از مطالبی که در این کتاب به آنها اشاره می‌شود عمدتاً برای مخاطبین غربی معنی دار است. نظر به اینکه قصد مترجم این بوده تا در حدامکان مطالب ذکر شده در این کتاب روشن باشد، لذا اضافاتی را بصورت زیرنویس به آن افزوده تا شاید آنها را برای خوانندگان جوانی که با این مطالب کمتر مأنوس هستند روشن‌تر کند.

تاریخ و سلسله مراتب رخدادها از مهمترین ارکان هر علمی به حساب می‌آید. مهم است تا هر شخصی تاریخ موضوع مورد علاقه خود را در حد امکان بداند، حال تفاوتی هم ندارد که این موضوع چه باشد (هنر، ادبیات، علم ...). از اینرو حداقل کاری که مترجم می‌توانسته انجام دهد افزودن تاریخ تولد و یا وفات اشخاصی بوده که در این کتاب به آنها اشاره شده، تا نوعی بینش تاریخی به خواننده داده باشد.

در پایان لازم میدانم از تمام کسانی که در ترجمه این کتاب مشوق من بودند تشکر کنم، مخصوصاً خانواده عزیزم.

تابستان 1386

کامران بزرگزاد ایمانی

پیش‌گفتار

$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image001.jpg$

در طول چند سال اخیر ما شاهد موج عظیمی از کتاب‌ها و برنامه‌های تلویزیونی هستیم که در آنها سعی می‌شود نظریه‌های جدید علمی بصورتی عرضه شود تا برای طیف گسترده‌ای از مخاطبین قابل فهم باشد. بنابراین آیا هیچ نیازی به کتاب دیگری در باره موضوعاتی از قبیل فضا، زمان و یا منشاء جهان، که اینقدر به آنها پرداخته شده، احساس می‌شود؟ چندی پیش در ایتنرنت مشغول جستجو در صفحات پرشمار کتابهای علمی بودم. موضوع جستجوی من کتاب‌هایی بود که در عنوان خود کلمه «زمان» را داشته باشد. دراین جستجو من تعداد 29 عنوان کتاب را پیدا کردم! که البته در میان آنها کتاب تاریخچه زمان استیون هاوکینگ [1] از همه معروف‌تر بود. ولی عناوین دیگری نیز بودند، مثلاً: درباره زمان، تولد زمان، لبه زمان، رودخانه زمان و غیره. بنظر می‌‌رسد در حال حاضر مورد سئوال قراردادن سرشتِ زمان، در بنیادی‌ترین سطح آن، مضوع اصلی بسیاری از کتاب‌ها قرار گرفته است. چیزی که مایه تعجب من شد این بود که می‌دیدم اکثر این آثار بعد از اینکه من شروع به نوشتن این کتاب کردم، چاپ شده بودند.

هنگامی که من در اواسط دهه 1980 دانشجوی دوره کارشناسی بودم، نویسندگان مطرح کتاب‌های علمی همچون پُل دیویس، جان گریبین و ریچارد داوکینز مایه الهام من بودند. ولی این نویسندگان تنها برای مومنان به علم، و قشر عمدتاً دانشجو، موعظه می‌کردند و در بهترین حالت، مخاطبین آنها «اشخاص‌ باهوش» بودند، حال این شخص باهوش هرکس که می‌خواهد باشد. بنابراین عمده‌ترین هدف من نوشتن کتابی در ابتدایی‌ترین سطح بود، که بعضی از طرز تفکر‌ها و نظریات فیزیک مدرن را برای همه شرح دهد، البته بشرط اینکه اصلاً انتخاب چنین کتابی (با این عنوان)، برای آنها به‌اندازه کافی جذابیت داشته باشد. همچنین سعی من این بوده تا با مخلوطی از سبک استیون هاوکینگ و همچنین تری پراچیت [2] کمی این کتاب را بامزه‌تر کنم (که احتمالاً خیلی دراین کار موفق نبوده‌ام).

بسیاری از دانشمندان این بحث را مطرح می‌کنند که وقتی موضوعات دشواری همچون نظریات نسبیت اینشتین زیاد از حد «ساده نویسی» ‌شود، به چنان سطحی تنزل پیدا می‌کنند که دیگر بیان آنها به این شکل صحیح نیست. من از اصطلاح «ساده نویسی» متنفرم. زیرا خیلی پرافاده بنظر می‌رسد. درحالیکه یک دانشمند فقط کسی است که سالهای زیادی را آموزش دیده تا مفاهیم مجرد، فرمولهای ریاضی و اصطلاحات تخصصی مربوط به رشته خود را بفهمد، این اصطلاح طوری وانمود می‌کند که آنگار آنها خیلی باهوشتر از بقیه هستند. قسمت مشکل در نوشتن این نوع کتاب‌ها تنها این است که این مفاهیم، بصورت طرح‌ها و کلماتی برگردانده شود تا همه اشخاصی که چنین دوره‌های تخصصی را ندیده‌اند بتوانند آنها را بفهمند.

این کتاب طوری نوشته شده که مخاطبین اصلی آن نوجوانان باشند. باوجود این هرکسی که عنوان این کتاب برایش گیرا و فریبنده باشد، می‌تواند از آن استفاده کند و مهم هم نیست که شما از دوران دبیرستان به بعد هیچگونه کتاب علمی نخوانده باشید.

چطور شد که این کتاب را نوشتم؟ خوب، درحدود سه سال قبل، بیل گلِتی، رئیس گروه فیزیک دانشگاه سُری، به من پیشنهاد کرد تا برای دانشجویان سال اول کارشناسی سخنرانی‌هایی را ترتیب دهم که موضوعات عمومی و جالب فیزیک مدرن، از جمله «کرم‌چاله‌ها»، را دربرگیرد. قطعاً چنین مواردی جزء موضوعات عمومی دوره کارشناسی فیزیک نبود. درحقیقت بدلیل مبحث جدید و کمتر شناخته شده کرم‌چاله‌ها، طرفداران سریال‌ تلویزیونی اِستار ترِک [3] (پیشتازان فضا) از این موضوع بیشتر آگاه بودند تا یک فیزیکدان معمولی. به هرحال من فکر کردم که این موضوع بامزه‌ای برای سخنرانی می‌شود و مقدمات آن را فراهم کردم. روزی متوجه شدم در میان حضار اشخاص زیادی حضور دارند که اصلاً دانشجوی این رشته نبودند، از جمله پژوهشگران دوره دکترا و همچنین کارمندان دفتری دانشگاه. بنظر می‌رسید چیزی سحرآمیز در عنوان این مبحث وجود داشته که موجب گردهم‌آیی این جمع ناهمگون شده است.

هر سال گروه فیزیک دانشگاه ما، فهرستی از اسامی سخنرانان و همچنین عنوان سخنرانی آنها را برای مدارس محلی و دانشگاه‌ها می‌فرستد. این کار برای گروه ما عمدتاً یک فعالیت تبلیغاتی محسوب می‌شود، تا مشوقی برای جذب دانشجویان جدید باشد. عنوانی که من برای سخنرانی خودم انتخاب کردم «کرم‌چاله‌ها» بود. از این موضوع چنان استقبالی بعمل آمد که موسسه فیزیک از من خواست در سال 1998 در کلیه مدارس کشور سخنرانی کنم. برای این کار من می‌بایست سفرهای زیادی را در سراسر کشور انجام می‌دادم تا در یک جمع چندصد نفری از دانش‌آموزان 14 تا 16 ساله سخنرانی کنم، و رویهم رفته مسئولیت سنگین‌تری را برایم بوجود می‌آورد. با توجه به مقدمات زیادی که برای انجام این سخنرانی‌ها بعمل می‌آمد، من پی بردم که دراین مدت حجم موارد جالب‌توجه چنان زیاد شده که دیگر نمی‌توان آنها را در طی یک سخنرانی یک ساعته عرضه کرد، و بنابراین تصمیم گرفتم آنها را در غالب یک کتاب بگنجانم.

سعی من این بوده که تا آنجا که ممکن باشد جدیدترین مطالب را عرضه کنم. درحقیقت، هنگامی که ناشر نسخه دستنویس را برای غلط گیری و بازبینی نهایی به من داد، مجبور شدم فصل مربوط به کیهان‌شناسی را بطور کامل اصلاح کنم. برطبق آخرین کشفیات نجومی، بسیاری از نظریات در مورد اندازه و شکل جهان درطول چند ماه اخیر چنان تغییر کرده که من فصل مربوط به آنها را بطور کامل باز نویسی کردم.

جیم الخلیلی

پورت‌موث، انگلستان، جولای 1999

مقدمه

$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image002.gif$

شیرماهی گفت «زمان آن رسیده تا درمورد چیزهای زیادی صحبت کنیم.»

« از درون آینه» نوشته لوئیس کارول [4]

... از اتم‌ها، ستارگان و کهکشان‌ها صحبت کنیم، و ببینیم سیاه‌چاله یعنی چه؛ و اینکه آیا برای ساختن یک ماشین‌ زمان، فضای اینشتین می‌تواند به اندازه‌ کافی خم شود یا نه.

مخاطبین این کتاب کسانی هستند که کنجکاوند تا در مورد مفاهیم عجیبی همچون سیاه‌چاله‌ها، خم شدن فضا، انفجار بزرگ، سفر در زمان و جهان‌های موازی چیزهایی بدانند، و تا آنجا که می‌دانم این شامل بیشتر افراد می‌شود. در هنگام نوشتن این کتاب من از خودم این سئوال را پرسیدم که آیا افراد کاملاً عادی می‌توانند در مورد بعضی از مفاهیم فیزیک مدرن چیزهایی بیاموزند، بدون اینکه قبل از قدم نهادن دراین راه نیازی به برآورد ضریب هوشی خود کنند.

موضوع اصلی این کتاب در سطوح گوناگونی در کتابهای دیگری نیز مطرح شده است. در بالاترین سطح، متون پیشرفته و رساله‌هایی قرار دارند که برای متخصصین این حوزه نگاشته می‌شود. اینها کتابهای سحری آمیزی هستند که تنها برای تعداد معدودی از متخصصین قابل فهمند. پس از آن کتابهای درسی دانشگاهی قرار دارد که مخاطبین آن عمدتاً دانشجویان فیزیک هستند. این سطح نیز حاوی بسیاری از موارد پیچیده است، اگرچه نه به دشواری سطح قبلی. در پائینترین سطح، کتابهای عامه-فهم علمی قرار داردند. مخاطبین این دسته کتابها اشخاص غیر متخصص هستند. دراین کتابها اثری از ریاضیات نیست و یا کم هست. ولی این نوع کتابها تنها برای این دو دسته می‌تواند جالب باشد: 1- آنهایی که درحوزه‌های دیگری از علوم فعالیت می‌کنند. و یا 2- طرفداران این نوع موضوعات که بطور ثابتی کتابهای مشابه را نیز مطالعه می‌کنند.

بنابراین، در هنگام نوشتن این کتاب تلاش زیادی کردم تا در حد امکان از زبان فنی استفاده نکنم. معمولاً این روزها اکثر نویسندگان کتابهای عامه پسند علمی، در بیان مفاهیم پیچیده فنی به زبان ساده، استاد شده‌اند. ولی گاه‌به‌گاه بعضی از این «اصطلاحات فنی»، که برای ما دانشمندان چیزی مانوس و عادی بنظر می‌رسد، از زبانمان می‌لغزد و فراموش می‌کنیم که این اصطلاحات برای هر کسی آن معنی را ندارد که برای ما دارد.

ده دقیقه کوتاه یا بلند؟

یک روز تابستان، هنگامی که ده یازده سال بیش نداشتم، مجذوب مفهوم زمان شده بودم. زمان از کجا می‌آید؟ آیا ساخته خود ماست یا قبلاً هم وجود داشته؟ آیا آینده از قبل در جایی وجود دارد؟ آیا این گذشته است که هنوز خودنمایی می‌کند؟ سئوالاتی که برای یک بچه بسیار سخت بود. ولی قبل از اینکه شما مرا با یک کودک نابغه اشتباه بگیرید، اجازه بدهید تا تصوری را که در آن هنگام از سفر در زمان داشتم با شما مطرح کنم. من می‌دانستم که در آن سوی دنیا، جایی در وسط اقیانوس آرام، خطی نامریی وجود داشت که از قطب شمال تا قطب جنوب امتداد می‌یافت و جهان را به دو قسمت امروز و دیروز تقسیم می‌کرد! اگر یک کشتی در میان این خط لنگر می‌انداخت آنگاه مثلاً در یک سر کشتی ساعت 9 صبح روز سه شنبه بود و در سوی دیگر آن ساعت 10 صبح روز دوشنبه. به طور قطع این مثال روشنی از سفردرزمان بود که تنها می‌شد با پیمودن چند قدم در طول عرشه کشتی از امروز به دیروز سفر کرد!

خوب، من می‌دانستم چیز مشکوکی در اینجا وجود دارد و بخاطر دارم شبی پدرم برایم توضیح داد که خطوط زمانی دور کره زمین ابداع خود انسان هستند. برای مثال اگر مقرر شود که هنگام نیمه شب در نیویورک ساعت پنج صبح در لندن باشد، این تنها به این دلیل است همانطور که زمین در حال چرخش است و کشورهای مختلف در مقابل خورشید قرار می‌گیرند، مطمئن شویم ساعات روز دقیقاً برای همه یک شکل باشد، و نه اینکه در همه‌جا ساعت یکسان باشند. من هم برای سفر در زمان، به نحوی، همین خط را در استدلال خود دنبال کردم، که بعداً موجب ناامیدی من شد. قطعاً مفهوم زمان فراتر از این بود، چیزی بسیار مرموزتر. من نظریه دیگری نیز در مورد سرعت گذشت زمان داشتم که بستگی کامل با حوصله‌ام داشت. آشکارا زمان در ساعات پایانی کلاس آهسته‌تر می‌شد و هنگامی که به موعد جشن تولدم نزدیکتر می‌شدیم، روزها و هفته‌ها در جای خود منجمد می‌شدند.

حالا نوبت فرزندان من است که به این قبیل نتایج برسند. اگر من به آنها بگویم که تنها ده دقیقه وقت دارند تا با اسباب بازیهای خود بازی کنند، آنگاه، آنها خیلی جدی خواهند پرسید که آیا ده دقیقه کوتاه، بلند یا متوسط. بهر حال، چه کسی می‌تواند منکر مشاهدات ساده‌ای باشد که گویای این ‌است که برای یک بچه زمان آهسته‌تر می‌گذرد. یک سال برای یک بچه پنج ساله مدت زمان خیلی زیادیست، زیرا این مدت دربردارنده یک پنجم طول زندگی اوست، ولی هر چقدر که ما پیرتر می‌شویم سالها مانند برق سپری می‌شوند، و به همین دلیل عباراتی مانند زیر را خیلی بکار می‌بریم: «باورتان می‌شود ؟ انگار همین دیروز بود که سال نو بود! » یا «واقعاً سه سال پیش بود که من برای آخرین بار اینجا بودم؟» و غیره.

اساساً ما حس می‌کنیم که این را می‌دانیم که زمان با سرعت ثابتی می‌گذرد. هنگامیکه ما می‌پرسیم که زمان با چه سرعتی میگذرد، پاسخ معمول و غلط انداز دانشمندان اینست که زمان با سرعت یک ثانیه در ثانیه می‌گذرد. فارغ از احساسات ذهنی که ما درمورد گذر زمان داریم، بر پایه باورهای دیرین خود می‌دانیم که یک ساعت کیهانی وجود دارد که اندازه ثانیه‌ها، دقیقه‌ها، ساعات، روزها و سالها را در جهان هستی بطور بی‌وقفه و بی‌امانی مشخص می‌کند وآن چیزی نیست که ما بتوانیم در آن تغییری بوجود آوریم.

یا شاید چیزی هست که بتوانیم در آن تغییری بوجود آوریم؟ آیا این چنین ساعت کیهانی واقعاً وجود دارد؟ فیزیک مدرن نشان داده است که این چنین چیزی (ساعت کیهانی) وجود ندارد. نگران نباشید، شواهد بسیار محکمی برای پشتیبانی از این امر وجود دارد. در واقع، قبل ازاینکه به مطلب دیگری بپردازم، این مورد را بعنوان مقدمه ذکر می‌کنم: ما اطمینان داریم که سفر در زمان به طرف آینده امکان پذیر است. دانشمندان آزمایشات زیادی را با موفقیت انجام داده‌اند که بدون شک ثابت کننده این مورد است. درصورتی که شما هرگونه تردیدی در مورد این مطلب متحیر کننده و شاید هول آور دارید، دلیل آن این نیست که دولت‌های حساس و سانسورچی برای امنیت ملی خود این حقیقت را ازشما مخفی نگاه داشته‌اند، بلکه بخاطر این ‌است که شما هیچگاه در یک کلاس که نسبیت خاص را برای شما شرح دهد شرکت نکرده‌اید، و آن قسمتی از چیزیست که من امیدوارم در این کتاب برای شما بازگو کنم.

عقل سلیم (حواس معمول)[5]

شاید صحیح باشد که بگوییم بیشتر افراد خیلی با تئوری‌های [6] نسبیت اینشتین میانه خوبی ندارند. برای همین است هنگامیکه با دوستان غیرمتخصص خودم در باره اینکه هیچ چیز نمی‌تواند سریعتر از نور حرکت کند گفتگو می‌کنم، هیچ موقع از عکس‌العمل آنها متعجب نمی‌شوم. آنها می‌گویند «شما از کجا می‌دانید؟ اینکه دانشمندان هنوز چیزی را پیدا نکرده‌اند که بتواند سریعتر از نور حرکت کند دلیل بر این نمی‌شود که اینچنین چیزی بعداً یافت نشود و شما مجبور به پس گرفتن گفته‌های خود شوید. شما باید ذهن خود را در مقابل امکان وقوع رویدادهایی که برای شما روی نداده بیشتر باز نگاه دارید. فکر کنید که تلویزیون را به یک قبیله دور افتاده ساکن آمازون نشان بدهید آنها پیش خود چه فکر می‌کنند ...» و از این قبیل حرف‌ها. حداقل من‌یکی از این پاسخها ناراحت نمی‌شوم، بدلیل اینکه این دقیقاً همان روحیه‌ای است که انتظار دارم خواننده این کتاب دارا باشد. یعنی، گشاده ذهن باشد و قابلیت این را داشته باشد تا جهان‌بینی‌های نوین را پذیرا باشد، حتی اگر آن نظرات برخلاف تمام چیزهایی باشد که شما به آنها اطمینان دارید؛ یعنی آن چیزهایی که عقل سلیم نامیده می‌شوند.

زمانی از آلبرت اینشتین نقل می‌کنند که گفته بود «عقل سلیم تنها یک پیشداوری است که ما آن را تا سنین هجده سالگی کسب می‌کنیم». بنابراین، برای آن قبیله نشین‌های آمازونی که قبلاً هرگز تلویزیون ندیده‌اند، این جعبه که می‌تواند با آنها صحبت کند و دنیایی را به آنها نشان دهد، برخلاف عقل سلیم آنهاست (بسیار خوب، من فرض می‌کنم که آنها برق دارند!). ولی مطمئن هستم که شما نیز موافقید که پس از اینکه مدتی را با این قبیله سپری کردیم و برای آنها در مورد امواج رادیویی و الکترونیک جدید و دیگر مواردی که موجب ساخت و کارکرد تلویزیون می‌شود توضیح دادیم، آنگاه آنها نیز کم‌کم مجبورند تا بینش خود از جهان را بصورتی تغییر دهند تا این اطلاعات جدید تضادی با عقل سلیم آنها نداشته باشد.

در آغاز قرن بیستم چندین نظریه جدید علمی توسعه داده شدند که صحت آنها، حداقل تاکنون، مورد تائید بوده ‌است. در میان اینها نظریاتی هستند که پایه تقریباً تمامی علوم و فنون جدید را تشکیل میدهند. این حقیقت که ما ساعتهای دیجیتال، کامپیوتر، تلویزیون، اجاق مایکرو ویو، دستگاه‌های پخش سی‌دی و تقریباً هر وسیله مدرن دیگری داریم، گواهی بر این مدعا است که این نظریات، اگرچه نه تمام آنها، بلکه قسمت مهمی از آنها در توصیف جهان اطراف ما موفق بوده‌اند. نظریات مورد بحث یکی نظریه نسبیت و دیگری مکانیک کوانتوم می‌باشد. باید این مسئله را ذکر کنم که موفقیت یک نظریه درآن است که بتواند پیش‌بینی کند که تحت شرایط معینی چه اتفاقاتی روی خواهد داد. مثلاً بگوید : اگر مطابق این نظریه این کار را انجام دهید، آن اتفاق روی خواهد داد. اگر من اقدام به آزمایشی بکنم و دریابم که پیش‌بینی‌های نظریه درست از آب درمی‌آیند درآن صورت این دلیلی است برای تائید نظریه. ولی نظریه با قانون متفاوت است.

قانون جاذبه می‌گوید که تمام اشیاء در جهان هستی همدیگر را با نیرویی جذب می‌کند که میزان آن بستگی به جرم دو جسم و فاصله آنها از یکدیگر دارد. این موضوع چیزی نیست که قابل تردید باشد و درحالیکه ما می‌دانیم این قانون در مواقعی که با اجرام بسیار سنگینی همچون سیاه‌چاله‌ها سروکارداریم باید تعدیل شود، هنگامی که موقع توصیف سقوط اجسام بر روی زمین باشد، بطور کامل به آن اطمینان می‌کنیم. ولی یک نظریه تازمانی خوب محسوب می‌شود که نظریه بهتری آن را رد نکند. ما هیچگاه نمی‌توانیم صحت یک نظریه را اثبات کنیم، بلکه می‌توانیم آن را رد کنیم و نظریه موفق آن است که در طول زمان دوام بیشتری داشته باشد. برخلاف نظر بسیاری از اشخاص غیرمتخصص، بیشتر دانشمندان به چیزی جز اثبات نادرست بودن یک نظریه علاقه ندارند، هر چقدر آن نظریه آبرو و احترام بیشتر داشته باشد، بهتر. بنابراین، بدلیل اینکه نظریاتی از قبیل نسبیت آینیشتین و مکانیک کوانتوم، علی‌رقم کوششهای مستمری که فیزیکدانان در طول قرن بیستم در رد آنها، یا حداقل پیدا کردن نقایصی در آنها بعمل آورده‌اند، توانسته‌اند دوام بیاورند، ما مجبوریم تائید کنیم که احتمالاً آنها درست هستند، ویا حداقل در مسیر درستی گام برمی‌دارند.

بازگشت به آینده

ببخشید از بحث اصلی دور شدیم. باید به موضوع جالب امکان سفر در زمان بازگردیم. بعداً دراین کتاب با جزئیات بیشتری شرح خواهم داد که نظریه نسبیت درمورد چیست. در ضمن در اینجا مثالی را از اینکه نسبیت چه چیزی را به ما می‌آموزد می‌آورم: اگر شما در سفینه‌ای که می‌تواند با سرعت نزدیک به سرعت نور حرکت کند سوار شوید و با سرعتی زیاد، گشت کوتاهی، مثلاً بمدت چهار سال، در کهکشان بزنید، آنگاه هنگام بازگشت به زمین شما کمی حیرت زده خواهید شد. اگر تقویم سفینه شما هنگام عزیمت از زمین تاریخ ژانویه 2000 و هنگام بازگشت ژانویه 2004 را نشان دهد، درآن صورت بسته به سرعت و مسیری که در میان ستاره‌ها داشته‌اید، طبق تقویم زمینی اکنون سال 2040 است و همه چهل سال پیرتر شده‌اند. آنها نیز، برطبق تقویم‌شان، به همان اندازه از اینکه شما چقدر جوان مانده‌اید حیرت زده خواهند شد.

بنابراین تقویم سفینه شما، هنگام سفر با سرعتهای خیلی زیاد، چهار سال را اندازه گرفته در صورتیکه تمام ساعتهای موجود در زمین 40 سال را اندازه گرفته اند. این امر چگونه ممکن است؟ آیا واقعاً زمان در درون سفینه شما، به بدلیل داشتن سرعت بالا، کند شده است؟ اگر اینچنین باشد، این به این معنی است که، بهر دلیل و منظوری، شما سی‌وشش سال به طرف آینده پرتاب شده‌اید.

اگرچه من بعداً به این مسئله باز خواهم گشت، ولی ایده کند شدن زمان، هنگام حرکت با سرعتهای بالا، چیزی است که حقیقتاً بررسی شده و بارها با آزمایشات گوناگون با دقت زیادی مورد تائید قرار گرفته است. برای مثال، دانشمندان قبل از انجام آزمایشی، دو ساعت اتمی با دقت بسیار بالا را با هم روی یک زمان تنظیم می‌کنند، آنگاه یکی از آنها را در درون یک هواپیمای جت قرار میدهند. هنگامی که هواپیما پس از یک سفر کوتاه به زمین بازمی‌گردد، دو ساعت را با هم مقایسه می‌کنند. مشاهده شده است ساعتی که در هواپیما قرار داشته به مقدار بسیار اندکی درمقایسه با ساعتی که بیحرکت روی زمین مانده، عقب‌تر است. اگر بخواهیم سفینه‌ای که با سرعتی نزدیک به سرعت نور حرکت می‌کند، و هواپیمایی که با سرعت هزار کیلومتر در ساعت درحرکت است را با یکدیگر مقایسه کنیم، باید توجه داشته باشید که علی رقم سرعت نسبتاً کم هواپیما در مقایسه با سرعت سفینه (که حدود یک میلیون بار بیشتر است)، تفاوت نامحسوس، ولی اندک، این دو ساعت بایکدیگر، چیزیست جدی و واقعی. این ساعتها بقدری دقیق هستند که ما نمی‌توانیم شکی در مشاهده و یا نتیجه‌گیری خود بکنیم.

خوانندگانی که تا حدودی با نسبیت آشنایی دارند ممکن است بخواهند این موضوع را مطرح کنند که مثال سفینه به این سادگی هم که من بیان کردم نیست. این مسئله درست است، ولی ریزه‌کاری‌هایی که به نام پارادوکس ساعت مشهور است باید بماند تا زمانی که ما در فصل 6 مبحث نسبیت خاص را توضیح دهیم. فعلاً مسئله را در سطح ساده، ولی کاملاً صحیح خود، نگاه می‌داریم و می‌گوییم حرکت با سرعتهای بسیار بالا، اجازه سفر به آینده را به ما می‌دهد.

در مورد سفر به زمان گذشته چطور؟ در بسیاری از موارد سفر به گذشته بسیار جذابتر از سفر به آینده است. ولی مشخص شده که این حالت بسیار سخت‌تر از حالت قبلی می‌باشد. ممکن است این مورد برای شما شگفت آور باشد که سفر به آینده آسانتر از سفر به گذشته است. دلیل شگفتی شما این است که شاید تصور می‌کنید مفهوم سفر به آینده جالب‌تر از سفر به گذشته است. گذشته ممکن است غیر قابل دسترس باشد، ولی در هر حال وجود دارد چون قبلاً اتفاق افتاده. در مقابل، آینده قرار است که اتفاق بیفتد. شما چگونه می‌توانید به زمانی سفر کنید که هنوز اتفاق نیفتاده؟

حتی بدتر از این، اگر شما به این مسئله اعتقاد دارید که تا حدودی سرنوشت خود را تحت کنترل دارید [7] آنگاه تعداد بیشماری از آینده می‌تواند برای شما وجود داشته باشد. بنابراین چه چیزی مشخص می‌کند که شما به کدام یک از این آینده‌ها سفر می‌کنید؟ البته رسیدن به آینده (بوسیله حرکت با سرعت بالا) مستلزم این نیست که در آنجا آینده‌ی در انتظار شما باشد. این تنها به این معنی‌است که شما از چهارچوب زمانی اطراف خود خارج شده و به چهارچوب زمانی خواهید رفت که آهسته‌تر حرکت می‌کند. تا هنگامی که شما در این‌حالت بسر می‌برید، زمان در خارج از این چهارچوب سریعتر می‌گذرد و آینده با سرعت بیشتری در مقابل شما آشکار می‌شود. هنگامی که به چهارچوب قبلی خود باز می‌گردید، شما خیلی سریعتر از دیگران به آینده رسیده‌اید. این تاحدودی شبیه به این ‌است که شما پس از گذشت چند سال از حالت اغماء خارج شوید و با خود فکر کنید که تنها چند ساعت بر شما گذشته است. تفاوت این دو حالت اینست که شما پس از خروج از حالت اغماء به سراغ آینه می‌روید و با حیرت می‌بینید که صورتتان چند سال پیرتر شده، درصورتیکه هنگام بازگشت از یک سفر (با سرعتهای بسیار بالا)، شما از اینکه دیگران پیرتر شده‌اند و خودتان (و هرآنچه در این سفر به همراه شما بوده) جوان مانده‌اید حیرت خواهید کرد. چیزی که واقعاً بنظرتان عجیب خواهد رسید این ‌است که شما هنگامی که با این سرعت بالا در حرکت بوده‌اید چیز متفاوتی را مشاهده نکرده‌اید. از نظر شما، زمان با آهنگ معمولی خود، طبق ساعتی که در سفینه شما قرار دارد، می‌گذرد و اگر قادر باشید که از پنجره‌ای به بیرون از سفینه نگاه کنید، بصورت متناقضی خواهید دید که در بیرون زمان کندتر می‌گذرد!

البته مشکلی در این میان وجود دارد و آن این ‌است که هنگامی که شما به آینده رسیدید، در آنجا گیر خواهید افتاد و امکان بازگشت به آن «زمان حالی» را که از آن آمده‌اید نخواهید داشت. تاریخی که شما با سفینه خود از آن عزیمت کردید اکنون گذشته شما محسوب می‌شود و سفر به گذشته تا حدودی مشکل است. ولی اینکه آن را مشکل بدانیم، تا آنکه آن را ناممکن بخوانیم دو چیز متفاوت‌اند.

با خودتان ملاقات کنید

نمونه‌های گیج‌کننده‌ای وجود دارد که گویای اینست که اگر سفر به گذشته ممکن باشد، چیزها چقدر مضحک میشوند و تعداد آنها بقدری زیاد است که من می‌توانم با ذکر آنها این کتاب را پر کنم. برای مثال، حالتی را در نظر بگیرید که سفر به گذشته ممکن است و شما تصمیم می‌گیرید به گذشته رفته و نمونه جوانتر خود را ملاقات کنید، و زمان این ملاقات هم هنگامی است که او می‌خواهد در بازار بورس روی سهامی سرمایه گذاری کند که شما از قبل می‌دانید این سرمایه‌گذاری با شکست مواجه خواهد شد. اگر شما بتوانید نمونه جوانتر خود را متقاعد کنید که دست به اینکار نزند، در آن صورت احتمالاً زندگی‌تان بکلی با آنچه که اکنون هست متفاوت خواهد بود. در زمانی که شما به سن کنونی خود برسید و بخواهید به گذشته بروید و از انجام سرمایه گذاری جلوگیری کنید، دیگر نیازی به اینکار نخواهید دید، برای اینکه اصلاًً سرمایه گذاری انجام نشده. بنابراین شما به گذشته سفر نمی‌کنید. ولی درعین حال شما باید پولی را که از عدم سرمایه گذاری قبلاً داشته‌اید، هنوز هم داشته باشید چون نمونه پیرترتان آمده و به شما گفته که پول خود را هدر ندهید. شما اکنون در جهانی زندگی می‌کنید که مصمم هستید که سرمایه گذاری نکنید. آیا دلیل این امر آن بوده که قبلاً با نمونه پیرتر خود ملاقات کرده‌اید؟ اگر چنین بوده، پس شما حتماً سفری به گذشته داشته‌اید.

اگر بکلی با آنچه که تا بحال خوانده‌اید گیج شدید، نگران نباشد، باید هم اینطور باشد. نکته اصلی این پارادوکس (معمای متناقض) در همینجاست. اگر شما برای آگاه کردن خودتان در مورد چیزی به گذشته سفر کنید، آنگاه دو اتفاق ممکن است بیفتد. اولاً این حقیقت که شما تصمیم دارید به گذشته رفته‌ و از انجام چیزی جلوگیری کنید به این معناست که آن چیز اتفاق افتاده و شما در مورد متوقف کردن آن با شکست مواجه شده‌اید. در اینجا فقط یک روایت از تاریخ را داریم. ثانیاً، اکنون شما باید زمانی را بخاطر بیاورید که در گذشته از طرف نمونه پیرترتان با شما ملاقاتی انجام شده و شما می‌دانید که این ملاقات بیهوده بوده، و در نتیجه می‌دانید که انجام آن، ارزشش را ندارد. در اینجاست که شرح و بسط‌ها فرو می‌ریزد. اگر شما می‌دانید که فایده‌ای ندارد تا به گذشته بروید، و اینکار را هم نمی‌کنید، پس چه کسی اینکار را انجام داده؟ شما باید در زمان به عقب بازگشته باشید، بدلیل اینکه بخاطر دارید که ملاقاتی با نمونه پیرتر خود داشته‌اید و او سعی کرده است شما را از انجام عملی باز دارد. به قسمی، این به این‌معنی است که شما آزادی انتخاب عمل نداشته‌اید. پس چه اتفاقی افتاده است؟ آیا از جایی سروکله فرمانروای زمان پیدا شده و شما را مجبور کرده تا در ماشین زمان سوار شوید، و برای شما توضیح داده که اگر اینکار را انجام ندهید تار و پود فضا-زمان به هم خواهد ریخت؟

باوجود تمام این مسائل، ممکن است دانستن این مطلب برای شما جالب باشد که سفردرزمان به سوی گذشته در نظریه نسبیت عام اینشتین مجاز است، و این چیزیست که حدود 90 سال قبل کشف شد. همچنین، به دلیل اینکه فعلاً نظریه نسبیت عام بهترین نظریه درمورد ماهیت زمان است، تا هنگامی که نظریه بهتری پیدا نشده تا درک ما را از مفهوم زمان عمق بیشتری ببخشد، ما مجبوریم پیش‌بینی‌های این نظریه را جدی فرض کنیم. پس شما متعجب خواهید شد که چرا کسی تابحال قادر به ساختن ماشین زمان نبوده است؟ دراین کتاب، من با نزدیک شدن به بعضی از پرجاذبه‌ترین حوزه‌های فیزیک مدرن، جواب این سئوال را روشن خواهم نمود.

بعضی از چیزهایی که ما در مورد جهان هستی کشف کرده‌ایم بقدری حیرت‌آور و باورنکردنی هستند که من امیدوارم شما پس از مطالعه این کتاب احساس کنید با ندانستن آنها تاکنون چقدر در خواب غفلت بوده‌اید. چیزی که من می‌خواهم شما از این کتاب کسب کنید این ‌است که در احساس شگفتی من نسبت به کائنات با من شریک باشید. بعلاوه می‌خواهم هنگامی که بر سر میز شام نشسته‌اید و صحبتِ سفر در زمان پیش می‌آید، دلایل محکم علمی ارائه داده باشم تا شما را در این بحث، در برابر دوستانتان تقویت کند.

فصل 1

بُعد چهارم

$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image003.gif$

با اَشکال رابطه دارد

هندسه شاخه‌ای از ریاضیات است که با خواص و روابط مابین نقطه‌ها، خط‌ها، سطح‌ها و حجم‌ها سروکار دارد. شاید اکثر مردم مجدداً به آن چیزهایی که در مدرسه درباره هندسه آموخته‌اند فکر نکنند، چیزهایی مثل: مساحت دایره، طول اضلاع مثلث قائم‌الزاویه، حجم مکعب‌ها و استوانه‌ها. بگذریم از آن ابزارهای دوست‌داشتنی، نقاله و پرگار، که همیشه با دلتنگی به آنها نگاه می‌کنیم. بنابراین امیدوارم از اینکه بخشی از کتاب به هندسه اختصاص یافته، موجب انصراف شما از ادامه راه نشود.

درجهت تلاش‌هایی که در این کتاب در مورد خودداری از کاربرد زبان فنی می‌شود، من هندسه را به این صورت تعریف میکنم: هندسه چیزیست که با َاشکال رابطه دارد. بیایید تا منظور خودمان از شکل را در عمومی‌ترین صورت خود مشخص کنیم. به حرف «S» نگاه کنید: شکل این حرف یک خط منحنی است. یک لکه رنگ نیز دارای شکل است، ولی در آنجا این شکل بصورت یک خط نیست، بلکه ناحیه‌ای است که دارای سطح می‌باشد. اشیاء نیز دارای شکل هستند. مکعب‌ها، استوانه‌ها، انسان‌ها، ماشین‌ها همه اشکال هندسی هستند که حجم نامیده می‌شود.

خصوصیتی که وجه تمایز مابین این سه حالت مختلف (خط، سطح و حجم) است، در تعداد ابعادی است که برای مشخص کردن آنها بکار می‌رود. گفته می‌شود که خط یک-بعدی است، یا به اختصار 1D، سطح دو-بعدی است، یا 2D و به همین ترتیب حجم سه-بعدی است یا 3D.[8]

آیا دلیلی وجود دارد که من نتوانم از ابعاد بالاتر نام ببرم؟ چه چیز بخصوصی در مورد عدد 3 وجود دارد که ما باید در آنجا متوقف شویم؟ البته جواب این سئوال این ‌است که ما در جهانی زندگی می‌کنیم که سه بُعد فضایی دارد، یعنی: ما می‌توانیم به جلو/عقب، چپ/راست و یا بالا/ پائین حرکت کنیم، ولی برای ما غیر ممکن است در جهت جدیدی حرکت کنیم که بر هر یک از این جهات عمود باشد. در ریاضیات، این جهات که ما آزاد هستیم در طول آنها حرکت کنیم، جهاتِ دو به دو عمود برهم نامیده می‌شوند.

تمام اشیاء اطراف ما سه بعدی هستند. کتابی که شما مشغول خواندن آن هستید، دارای ارتفاع، پهنا و ضخامت معینی است (تمام آن کمیتهایی که دارای طول هستند و در جهات عمود بر هم قرار دارند). این سه عدد با هم، ابعاد کتاب را معین می‌کنند. در حقیقت اگر شما این سه عدد را در هم ضرب کنید، حجم این کتاب حاصل خواهد شد. این حالت برای تمام اجسام قابل کاربرد نیست. برای مثال، در مورد کره تنها یک عدد برای مشخص کردن آن لازم است، که آنهم شعاع آن است. ولی این شکل هنوز هم یک شکل سه-بعدی بحساب می‌آید، زیرا یک جسم است که داری حجم است و در فضای سه-بعدی جا می‌گیرد.

ما در اطراف خودمان اشکالی را می‌بینیم که یک، دو و یا سه بعد دارند، ولی از چهار بعد خبری نیست زیرا چنان اشیائی نمی‌توانند در فضای سه-بعدی ما جای داده شوند. درحقیقت، ما حتی نمی‌توانیم اشکال چهاربعدی را پیش خود مجسم کنیم. مجسم کردن چیزی به این معنی است که ما در ذهن خود از آن چیز یک مدل بسازیم و ذهن ما تنها از عهپده حداکثر سه بعد برمی‌آید. در نتیجه ما حتی قادر نیستیم به یک چیز چهار بعدی فکرکنیم.

برای بسیاری از اشخاص «یک-بعدی» یعنی حرکت در یک جهت. اضافه کردن یک بُعد دیگر به یک چیز یعنی اجازه حرکت دادن به آن، در یک جهت جدید. شما ممکن است بگویید «این درست، ولی در مورد حرفS چطور؟». هنگامی که شما حرف S را می‌نویسید قلم شما یک منحنی را در جهات مختلف طی می‌کند، چگونه این شکل بوجود آمده هنوز یک-بعدی است؟ فرض کنید نقطه‌ای به نام فِرِد [9] روی یک خط زندگی می‌کند (شکل 1.1). فِرِد قادر نیست خارج از خط حرکت کند و حرکتش محدود به چپ و یا راست است. ولی اگر جهان او شبیه حرف S باشد چطور؟ حالا جهان او چند بُعدی است؟ جواب هنوز یک است. او هنوز مُقید است که تنها به بالا/پائین برود. مسلماً حالا که او باید مسیرهای خمیده را طی کند، زندگی او کمی جالبتر شده، ولی خمیدگی یک شکل تعداد ابعاد آن را زیادتر نمی‌کند. (ضمناً، بدلیل اینکه فِرِد خود یک نقطه است، برای اینکه تعریفی ریاضی از خود او بدهیم، باید بگوییم که او موجودی صفر- بُعدی است.)

روش دیگری که می‌توانیم در مورد ابعاد فضا از آن صحبت کنیم اینستکه ببینیم چند عدد لازم داریم تا موقعیت یک نقطه معین را در آن فضا مشخص کنیم. به این اعداد مختصات آن نقطه نیز میگویند. مثال زیر، که خاطرم هست چند سال قبل آنرا در جایی خواندم ولی یادم نیست کجا، هنوز هم یکی از بهترین نمونه‌هایی است که سراغ دارم. فرض کنید شما سوار بر قایق کوچکی هستید و روی یک رود باریک سفر می‌کنید. اگر نقطه‌ای را بعنوان نقطه مرجع انتخاب کنید (مثلاً دهکده‌ای که قبلاً از آن عبور کرده‌اید)، برای مشخص کردن موقعیت خود تنها به یک عدد نیاز دارید و آنهم فاصله‌ای است که شما تاکنون از آن نقطه دور شده‌اید. اگر تصمیم بگیرید برای ناهار توقف کنید و به یکی از دوستانتان با تلفن موقعیت خود را اطلاع دهید، تنها کافیست به او مثلاً بگویید که 6 کیلومتر از دهکده بالاتر رفته‌اید. این مهم نیست که چقدر این رودخانه پرپیچ و خم باشد، این 6 کیلومتر مشخص کننده یک مسیر مستقیم 6 کیلومتری نبوده، بلکه طول مسافتی بوده که شما (از دهکده) طی کرده اید. بنابراین ما می‌گوییم که حرکت این قایق محدود به یک بُعد است، اگرچه مسیر حرکت آن یک خط راست نباشد.

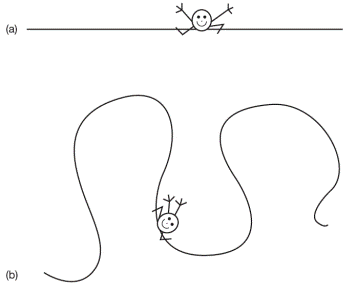
$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image004.gif$

شکل 1.1 - فِرِد نقطه‌ی است که روی یک جهان تک-بعدی زندگی می‌کند. در حالت (a) جهان او صاف و در حالت (b) جهان او خمیده است. (توجه داشته باشید، یک نقطه، دست‌وپا یا چشم‌ و ابرو ندارد، درغیر اینصورت یک شکل دو بعدی بحساب می‌آید!)

اگر شما سوار یک کشتی باشید که بر روی اقیانوس حرکت می‌کند چطور؟ اکنون شما به دو عدد (مختصات) نیاز دارید که موقعیت خود را مشخص کنید. این دو عدد عبارتند از طول و عرض جغرافیایی شما نسبت به یک نقطه مرجع، مثلاً نزدیکترین بندر، و یا مختصات ثابت بین‌المللی که برای همین کار مشخص شده. حالا کشتی در دو بعد حرکت می‌کند.

از سوی دیگر، برای یک زیردریایی شما به سه نقطه نیاز دارید تا موقعیت آن را دقیقاً مشخص کنید. علاوه بر طول و عرض جغرافیایی شما باید عدد دیگری هم برای بعد سوم مشخص کنید، و آن عمق زیر دریایی نسبت به سطح آب است. و بنابراین ما می‌گوییم که زیردریایی آزاد است که در فضای سه- بعدی حرکت کند.

فضا چیست؟

همه ما فکر می‌کنیم که می‌دانیم معنی «فضا» چیست. در جمله‌های مختلفی از فضا یاد می‌کنیم، مثلاً می‌گوئیم: «آن گوشه یک فضای خالی هست» یا «فضای خالی برای تکان خوردن نیست» ویا «فضا آخرین سنگر انسان است». هنگامی که ما مجبوریم به معنی فضا فکر کنیم، صرفاً آن را به معنی جایی برای قرار دادن اشیاء می‌انگاریم. چیزی که همه در آن باهم توافق داریم این ‌است که فضا به خودی خود چیزی نیست. ولی دراینصورت، آیا فضا می‌تواند بدون آنکه حاوی چیزی باشد وجود داشته باشد؟ یک جعبه خالی را درنظر بگیرید. حتی اگر ما تمام ملکولهای هوا را از داخل آن تخلیه کنیم، بصورتیکه واقعاً چیزی در آن نباشد، از اینکه می‌بینیم مفهوم فضا هنوز هم وجود دارد خرسند خواهیم بود. فضا در اینجا تنها به حجم جعبه دلالت دارد.

درصورتیکه فضا مرزی نداشته باشد تصور کردن آن مشکل است. ما فکر می‌کنیم که فضای داخل جعبه فقط به واسطه وجود خود جعبه وجود دارد. اگر ما دیواره‌های جعبه (درحقیقت مرز‌های آن) را برداریم آنگاه چه می‌شود؟ آیا هنوز هم فضایی وجود دارد؟ البته که وجود دارد، ولی حالا این فضا بخشی از یک ناحیه بزرگتر، مثلاً اطاقی که ما در آن هستیم، می‌شود. بیاید باهم چیز عجیبتری را بررسی کنیم: اساساً جهان هستی ما متشکل از یک فضای بسیار بزرگ است (و حتی ممکن است بی‌نهایت باشد) که حاوی حجم عظیمی از ماده است (کهکشان‌ها، ستارگان، سحابی‌ها، سیارات و غیره). اگر این جهان بکلی خالی از ماده بود چطور؟ آیا هنوز هم فضایی وجود داشت؟ جواب مثبت است، زیرا وجود فضا نیازی به وجود ماده در درون خود ندارد. در اینجا صحبت ما می‌تواند خیلی ساده به سوی یک موضوع بسیار فنی و دشوار (که هنوزهم بر سر آن بحث زیادی است) موسوم به اصل ماخ سوق داده شود - و چون در اینجا گرداننده بحث خودم هستم و بخوبی می‌دانم که چه چیزی را می‌خواهم مطرح کنم پس با هم به این سمت پیش می‌رویم. این اصل می‌گوید که فضا، یا حداقل فاصله‌ها و جهت‌های موجود در آن، درصورتیکه ماده‌ای در آن وجود نداشته باشد بی‌معنی می‌شود. بعلاوه، اینشتین در تئوری نسبیت خود نشان داد که فضا هم، مانند زمان، چیزیست نسبی. ولی من فعلاً نمی‌خواهم در این‌مرحله آغازی از کتاب وارد این مباحث پیچیده شوم و فرض را براین می‌گیریم که اگرچه فضا خود یک شئ نیست، ولی با این وجود باید یک چیزی باشد!

ولی اگر فضا یک شئ قابل لمس نیست، آیا ما می‌توانیم در برابر آن کنشی داشته باشیم؟ آیا ماده بر روی آن تاثیر دارد؟ این مسئله روشن شده که حقیقتاً ماده می‌تواند برروی فضا تاثیر داشته باشد؛ ماده می‌تواند فضا را خم کند!

در فصل بعدی من از شما خواهم خواست تا یک فضای سه-بعدی خمیده را مجسم کنید [10]. شما پیش خود فکر خواهید کرد که اینکار ساده‌ای است و مثلاً شما می‌توانید به‌آسانی این کتاب را خم کنید. ولی اینکار به این ساد‌گی هم نیست. چون منظور من این نیست که یک شئ سه-بعدی را در یک فضای سه-بعدی خم کنید، بلکه منظور من خم کردن خود آن فضای سه-بعدی است که این شئ در آن قرار دارد.

در مورد انحناء خط یک-بعدی که حرف «S» را تشکیل می‌دهد فکر کنید. ما به یک ورقه کاغذ دو- بعدی برای نوشتن «S» بر روی آن نیاز داریم. در اینجا ما می‌گوییم شکلی یک-بعدی در فضایی با ابعاد بیشتر محصور شده است. بطور مشابه، اگر ما بخواهیم خمیدگی یک ورقه کاغذ (فضای دو-بعدی) را مجسم کنیم نیاز به یک فضای سه-بعدی داریم. مشخص است که برای درک خمیدگی یک فضای سه-بعدی ما نیاز به فضای چهار- بعدی داریم که بتوانیم خمیدگی را در آن انجام دهیم.

اگر شما هنوز یک جسم خم‌شده در فضا را، با فضای خم شده اشتباه می‌کنید، پس برای روشن شدن مطلب، مثالی را در فضای دو-بعدی برای شما می‌آورم. مربعی را فرض کنید که روی یک تکه کاغذ کشیده شده است (شکل 1.2a). این مربع می‌تواند در درون این فضای دو بعدی (یعنی کاغذ) خم شود و شکل متفاونی را بوجود آورد. برای مثال تصور کنید که دو گوشه روبروی هم را بکشیم تا یک لوزی حاصل شود (شکل 1.2b) یا اینکه خطوط را بصورت منحنی بکشیم (شکل 1.2c). همه اینها بکلی متفاوت است با اینکه ما خود کاغذ را خم کنیم (شکل 1.2d). گرچه ما مانند دو شکل قبل آن را بصورت دیگری ترسیم نکرده‌ایم، و تنها فضایی را که مربع درآن جای دارد خم کرده‌ایم، در این حالت حتی از نظر ما نیز مربع خمیده بنظر می‌رسد.

جهان دو- بُعدی و موجودات دو- بُعدی

به دلیل‌اینکه برای ما غیر ممکن است تا فضایی را مجسم کنیم که در آن جهان سه-بعدی خم شده باشد، من از یک ترفند کارآمد استفاده می‌کنم. ما فعلاً یکی از ابعاد فضایی خود، مثلاً بُعد عمق را، برای سهولت کار کنار می‌گذاریم و یک دنیای فرضی دو-بعدی را در نظر می‌گیریم. اینگونه جهان‌ها قبلاً هم بوسیله بسیاری از نویسندگان دیگر مورد بررسی قرار گرفته‌اند و به آنها اسامی نظیر جهانتخت [11] ویا پِلیِن‌وِرس [12] داده شده. ساکنین چنین دنیاهایی همگی تخت و مسطح هستند، موجوداتی شبیه به ‌مقواهای بریده شده، که مُقید شده‌اند «در درون سطح»، و نه «بر روی آن»، حرکت کنند. آنها می‌توانند به بالا/پائین و چپ/راست حرکت کنند ولی نمی‌توانند خارج از سطح خود حرکت کنند، زیرا اینکار به حرکت در بعد سوم نیاز دارد که این برای آنها امکان پذیر نیست. حالا تصور بعد چهارم، که فهم آن برای ما موجودات سه-بعدی ممکن نیست (ولی برای درک خمیدگی فضای سه-بعدی به آن نیاز داریم) معادل است با فضای سه-بعدی برای این موجودات دو-بعدی. ما خود به این بعد سوم دسترسی داریم، اگرچه که ساکنان جهان دو-بعدی فاقد آن هستند.

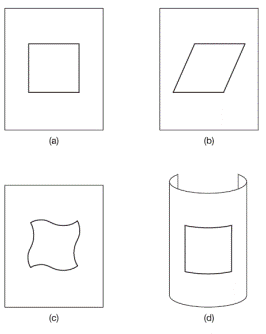
$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image005.gif$

شکل 1.2- (a) یک مربع، که شکلی است دو-بعدی، در یک فضای دو–بعدی رسم شده. در (b,c) مربع در درون فضای دربردارنده خود کج شده. در (d) خود فضای دربردارندهِ مربع (یعنی صفحه کاغذ) خم شده است.

اینچنین جهان دو-بعدی چگونه بنظر خواهد رسید؟ برای شروع، فکر بُعد سوم برای ساکنان آن دشوار است که تلاش در فکر کردن به بعُد چهارم برای ما. در شکل 1.3 چنین دو موجودی نشان داده شده. خیلی جالب است که ببینیم آنها چگونه وظایف اصلی خود را انجام می‌دهند. برای نمونه، چشمان آنها برای اینکه هر دو سمت را ببینند، حتماً باید بتواند از یک طرف به طرف دیگر بچرخد، اگر این حالت نباشد و هر یک از چشمان آنها در یک سمت سرشان قرار داشته باشد، گرچه می‌توانند هر دو سمت جلو و عقب خود را ببینند، ولی از یک توانایی اساسی بی‌بهره‌اند و آن توانایی نگاه کردن با دو چشم به یک جسم است. داشتن این ویژگی، همانطور که در مورد ما هم صادق است، آنها را قادر می‌کند تا در مورد فاصله اشیاء تصور درستی داشته باشند.

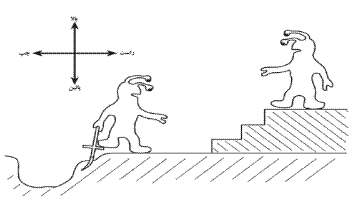
$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image006.gif$

شکل 1.3 موجودات دو بعدی آزادند که به بالا/پائین و چپ/راست حرکت کنند، ولی به بعد سوم، که معادل حرکت در خارج از صفحه است، دسترسی ندارند.

ولی اگر هر دو چشم آنها در یک سمت سرشان قرار میگرفت، آنها قادر نبودند پشت سر خود را ببینند، مگر اینکه هربار سروته شوند! این به‌این‌دلیل است که آنها قادر نیستند سر خود را بچرخانند، کاری که نیاز به حرکت در بُعد سوم (یعنی خارج از صفحه) دارد. این دو مشکل می‌تواند بصورتی حل شود که چشمان این موجودات آزاد باشند (به همان‌صورتیکه من در شکل نشان داده‌ام) به هر طرفی که می‌خواهند بچرخند. البته راه دیگر این ‌است که آنها دارای دو جفت چشم (چهار چشم) باشند که هرکدام در یک سمت سر آنها قرار گرفته باشد.

مشکل دیگری که ما با آن مواجه میشویم و در شکل 1.3 نشان داده شده است، این ‌است که چگونه آن موجود بالایی می‌تواند از موجود پائینی که گودالی را حفر کرده عبور کند. او نمی‌تواند از پهلوی او عبور کند، زیرا اینکار مستلزم خروج از صفحه است (خروج از دنیای آنها) و اینکار هم برای آنها ممکن نیست. شاید، همانطور که در شکل 1.4 نشان داده شده، در عرف آنها قراردادی وجود دارد که می‌گوید همیشه کسی که در سمت چپ ایستاده باید به کسی که در سمت راست ایستاده اجازه عبور دهد، و یا شاید عرفی وجود دارد که حکم میکند طبقه کارگر باید به طبقه اجتماعی بالاتر اجازه عبور دهد!

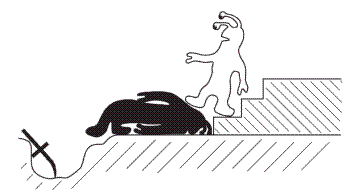
$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image007.gif$

شکل 1.4- این تنها راه ممکن است تا موجودات دو- بعدی بتوانند از مقابل یکدیگر عبور کنند. آنها نمی‌توانند از پهلوی یکدیگر عبور کنند، زیرا برای اینکار باید از صفحه خارج شوند.

یک وجه جالب توجه‌ در دنیای دو- بعدی‌ها آن‌چیزی است که در هنگام نگاه کردن به اشیاء می‌توانند ‌بینند. اول بیایید ببینیم هنگامی که خود ما به چیزی، مثلاً یک توپ، نگاه می‌کنیم چه چیزی را می‌بینیم. درحقیقت آنچه را که ما «می‌بینیم» یک تصویر دو-بعدی است که برروی شبکیه هریک از چشمان ما نقش می‌بندد و این‌مورد برای درک عُمق اشیاء برای ما بسیار اهمیت دارد. حتی اگر یکی از چشمانمان را نیز بسته نگاه داریم، بدلیل وجود سایه‌روشن‌های اطراف توپ، ما می‌دانیم آنچه که به آن نگاه می‌کنیم یک شئ سه-بعدی است نه یک شئ دو-بعدی مسطح مثل یک دایره. حتی گذشته از این، ما برطبق تجربیاتمان می‌دانیم که یک توپ چگونه بنظر میرسد و چگونه عمل می‌کند. بنابراین، وقتی به یک مسابقه فوتبال روی صفحه تلویزیون نگاه می‌کنیم، ما می‌دانیم که آن شئ دایره مانند که به آن ضربه زده می‌شود یک توپ فوتبال سه-بعدی است و نه یک قرص مسطح. علی‌رقم اینکه ما نمی‌توانیم هیچ سایه‌ای را در اطراف توپ مشاهده کنیم و برخلاف اینکه تصویر تلویزیون خود یک نگاشت دو- بعدی از یک واقعیت سه-بعدی است، ما واقعیت سه بعدی بودن تصویر توپ را بخوبی درک می‌کنیم.

هنگامی که ما به یک شئ سه-بعدی نگاه می‌کنیم تنها سطحی از آن را می‌بینیم که روبروی ما قرار دارد. حتی اگر نتوانیم پشت آنها را هم ببینیم، مغز ما درگیر عمل میشود و با توجه به تجربیات قبلی‌مان از اینچنین اشیائی، و همچنین چگونگی انعکاس نور از روی سطح آنها، مدل سه-بعدی کاملی از این شئ در ذهن ما ساخته می‌شود. چگونه می‌توانیم این را با آنچه موجودات دو-بعدی می‌بینند مقایسه کنیم؟ معادل کره (یا همان توپ) برای آنها دایره است. هنگامی که موجود دو-بعدی به یک دایره خیره می‌شود او تنها دارد به «لبه» آن نگاه می‌کند و بنابراین تنها نیمی از پیرامون آن را می‌بیند. او در «شبکیه» خود یک تصویر یک بعدی خواهد دید: یعنی یک خط راست. او هم برای درک انحناء این خط باید به سایه‌روشن‌های اطراف آن تکیه کند و همچنین باید دایره را بچرخاند تا ببیند این انحناء ادامه دارد و مطمئن شود که او در حقیقت یک چیز گِرد را می‌بیند. اگر فرضاً بوسیله یک خورشید دو-بعدی نوری از بالا براین دایره بتابد، درآن صورت قسمت بالایی روشنتر از قسمت پائینی که زیر دایره را تشکیل می‌دهد، خواهد بود. بنابراین، شکل یک دایره، برای یک موجود دو-بعدی، بکلی با آنچه ما از یک دایره در نظر داریم متفاوتند، زیرا آنها هرگز نمی‌توانند داخل دایره را ببینند. این وجه تمایزِ برتری است که ما نسبت به موجودات دو-بعدی داریم و می‌توانیم به داخل تمام اشیاء در دنیای آنها نگاه کنیم. این تنها شامل دایره نمی‌شود، بلکه ما می‌توانیم داخل بدن موجودات دو-بعدی را نیز ببینیم. تمام اعضاء بدن آنها برای ما آشکار است و این می‌تواند معنی جدیدی از عمل-قلب-باز[13] برای آنها داشته باشد. همانقدر که ما نمی‌‌توانیم داخل یک توپ را ببینیم، دیدن داخل یک دایره نیز برای موجودات دو-بعدی غیر ممکن است.

فرض کنید تصادفاً در جایی در جهان خودمان با این جهان-دو بعدی برخورد کنیم. اساساً، اگر جهان آنها مسطح باشد، آنگاه باید همچون یک صفحه‌ بی‌انتها، دنیای سه-بعدی مارا قطع کند. ولی بیایید فرض کنیم که دنیای آنها اندازه محدودی دارد (مثلاً به اندازه یک تابلو نقاشی) و ما در جایی به آن برمی‌خوریم. و فرض می‌کنم که می‌توانیم با ساکنان این دنیای دو-بعدی ارتباط برقرار کنیم.[14] همانطور که در شکل (1.5a) نشان داده شده، موجود دو-بعدی میخواهد یک شئ را از داخل مربع بردارد. او حتی نمی‌تواند شئ را ببیند و قادر نیست بدون اینکه مربع را پاره کند آن شئ را بدست بگیرد. برای ما نه فقط این شئ پیداست، بلکه اگر بخواهیم می‌توانیم به دنیای دو بعدی وارد شده، آن شئ را از قید دو بعد آزاد کنیم، و آن را به هرجایی که خواستیم در خارج از مربع انتقال دهیم (شکل 1.5b). ما به این‌دلیل می‌توانیم اینکار را انجام دهیم چون به بعد سوم دسترسی داریم.

پس از اینکه این موجود دو-بعدی را با ظاهر کردن یک شئ (یعنی تاج) از وسط آسمان ، وادار کردیم تا به قدرت مافوق‌ طبیعی ما اعتقاد پیدا کند، حالا می‌خواهیم با نشان دادن یک کُره، قدرت خارق‌العاده فضای سه بعدی را به رخ او بکشیم. البته ما برای اینکه او قادر باشد کُره را ببیند، آن را در صفحه او فرو خواهیم کرد و درصورتیکه شیئی (در آن صفحه) بر سر راهش نباشد از آن طرف صفحه بیرون خواهد آمد. درابتدا این موجود دو-بعدی نقطه‌ای را خواهد دید که بتدریج به خطی تبدیل می‌شود که هر دم درازتر شده، آنگاه یکباره کو‌تاه‌ شده و نهایتاً دوباره به یک نقطه تبدیل می‌شود و محو می‌گردد. با توجه به سایه‌هایی که در اطراف این خط است او نتیجه می‌گیرد خطی که او می‌بیند بخشی از پیرامون یک دایره است و می‌فهمد که به دایره‌ای نگاه می‌کند که بتدریج بزرگ شده و پس از اینکه به یک مقدار حداکثر رسید (هنگامی که کره تا نصفه در صفحه فرو رفته) دوباره کوچک شده و پس از آن از دنیای او محو می‌شود (وقتی کره از طرف دیگر صفحه خارج می‌شود). بنابراین همیشه این موجود دو-بعدی تنها سطح مقطعی از این گوی را خواهد دید.

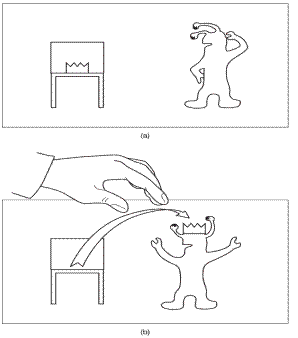
$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image008.gif$

شکل 1.5- (a) موجود دو-بعدی راهی برای دیدن تاجی که در درون مربع قرار داده شده ندارد، جز اینکه آنرا بشکند (یکی از خطوط آن را ببرد) و آژیر خطر را بصدا درآورد. (b) ما می‌توانیم با برداشتن این تاج از دنیای دو-بعدی و آوردن آن به بعُد سوم، به این دزد کمک کرده و آن را بر سر او بگذاریم.

فضای خمیده

همانطور که اشاره کردم این دنیای خیالی دو-بعدی لازم نیست که از نظر گستردگی نامتناهی باشد و بنابراین دارای لبه خواهد بود و خطوطی مرز‌های آن را مشخص خواهند نمود. ما بعداً خواهیم دید که جهان‌های مختلف حتماً دارای لبه و مرزی نیستند و بر این اساس، جهان دو-بعدی می‌تواند تا ابد ادامه داشته باشد. معلوم شده است که این حالت تنها درصورتی محتمل است که فضای دو-بعدی تخت و بدون انحناء باشد، و این همان چیزیست که من فرض کرده‌ام. ولی اگر ساکنان جهان دو-بعدی برروی سطح یک کره زندگی می‌کردند چطور؟ به هر حال سطح یک کره مساحت معینی دارد و بطور وضوح دارای هیچ حد و مرزی نیست، چون موجودات دو-بعدی می‌توانند در این‌جهان به هر طرفی بروند، بدون اینکه به نقطه‌ای برسند که فراتر از آن ممکن نباشد. نکته مهم و فریب‌دهنده‌ای که باید به آن اشاره کرد این ‌است که گرچه این جهان سطح یک کره ‌سه-بعدی است ولی از نظر این موجودات دو-بعدی، فضای درون کره و کلیه فضای خارج از آن لزوماً وجود ندارد. بنابراین در مقام قیاس، انسانهایی که بر سطح کره زمین زندگی می‌کنند نباید با این موجودات مقایسه شوند، زیرا بطور وضوح ما موجوداتی سه-بعدی هستیم که بر سطح یک شئ سه-بعدی زندگی می‌کنیم. موجودات دو-بعدی‌ تنها به سطح دو-بعدی روی کره دسترسی دارند و داخل آن حتی برای آنها وجود خارجی ندارد.

سئوال جالبی که مایلم اینجا مطرح کنم اینست که آیا این موجودات دو-بعدی می‌دانند که فضای آنها خمیده است.

یک راه برای آنها شبیه همان روشی است که ما با استفاده از آن می‌توانیم ثابت کنیم کره زمین‌ مسطح نیست: کسی را در یک جهت بخصوص به مسافرت می‌فرستیم و او نهایتاً دوباره، از جهت مخالفی که شروع به سفر کرده، به آن نقطه باز خواهد گشت. البته این روش دیگر منسوخ شده و ما اکنون بطور مرتب فضانوردانی را به فضا می‌فرستیم و آنها می‌توانند گرد بودن زمین را تصدیق کنند! ولی ساکنان جهان دو-بعدی نمی‌توانند به بالای دنیای خود بروند و از آن بالا به پایین نگاه کنند (چون محدود به سطح هستند). البته راه دیگری هم برای اینکه مشخص کنند جهان آنها خمیده است وجود دارد.

ما در مدرسه یاد گرفته‌ایم که اگر مجموع زوایه‌های یک مثلث را با هم جمع کنیم، همیشه عدد 180 درجه را بدست خواهیم آورد (شکل 1.6a). این مهم نیست که این مثلث چقدر بزرگ یا کوچک باشد و یا نوع آن چه باشد. اگر نوع مثلث قائم‌الزاویه باشد، در آن صورت مجموع دو زاویه غیرقائم باید 90 درجه باشد. اگر یکی از زوایا منفرجه باشد، مثلاً 160 درجه، آنگاه مجموع دو زاویه دیگر باید 20 درجه باشد. ولی قبل ازاینکه شما خیلی بی‌خیال این مسئله ساده هندسی شوید، اجازه دهید باگفتن مورد زیر، کمی موضوع را بامزه‌تر کنم: «مجموع زوایای یک مثلث فقط در صورتی 180 درجه می‌شود که آن مثلث روی یک سطح بدون انحناء رسم شود!». مثلثی که روی یک کره رسم شود، همیشه مجموع زوایای آن بیشتر از 180 خواهد بود. اینجا مثالی می‌آورم که منظورم را بیشتر روش کند. برای اینکار شما به یک کره و ماژیک نیاز دارید.

فرض کنید یک جهانگرد سفری را از قطب شمال شروع کرده و در مسیری مستقیم به سمت جنوب حرکت می‌کند، (در صورتیکه شما در قطب شمال باشید به هر سمتی که مستقیم حرکت کنید، آن سمت به طرف جنوب خواهد بود) آنگاه از بالای کانادا گذشته و در مسیری روبه پائین اقیانوس اطلس را طی می‌کند. او در نواحی شمالی برزیل به خط استوا خواهد رسید و آنگاه درآنجا، راه خود راکج کرده و از روی خط استوا مستقیم به سمت آفریقا حرکت می‌کند، و در آنجا به کِنیا می‌رسد و چون هوا خیلی گرم است دوباره مسیر خود را عوض کرده و بسمت شمال حرکت خواهد کرد و پس از عبور از اتیوپی، عربستان، خاورمیانه و شرق اروپا نهایتاً دو باره به قطب شمال باز می‌گردد.

اگر شما مسیر حرکت او را با ماژیک روی یک کره رسم کنید، آنگاه خواهید دید که او یک مثلث را طی کرده است (شکل 1.6b). با دقت به سه زاویه نگاه کنید. زوایایی که پهلوی خط استوا قرار دارند هر دو قائم‌الزاویه

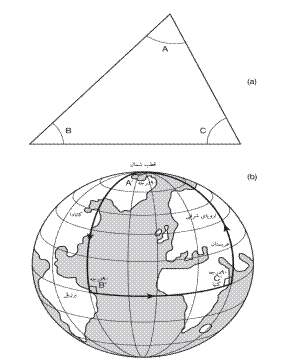
$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image009.gif$

شکل 1.6- (a) مجموعه زوایای مثلثی که برروی سطح یک کاغذ رسم شده برابر با 180 درجه است (A+B+C=180°). (b) در مثلثی که برروی سطح یک کره رسم شده، مجموع زوایا بیشتر از °180 است. آنچه در اینجا نشان داده شده سه زاویه °90 است.

(یعنی 90 درجه) هستند ولی زاویه‌ی هم که در بالا در قطب شمال قرار دارد، آن هم تقریباً نزدیک 90 درجه است و اگر ما این زوایا را با هم جمع کنیم حاصل چیزی حدود 270 درجه خواهد بود. این مثلث یک حالت خاص بود، ولی قاعده کلی این ‌است که مجموع زوایای هر مثلثی که برروی یک کره رسم شود بیشتر از 180 درجه خواهد بود. برای نمونه مجموع زوایای مثلثی که شهرهای پاریس، رم و مسکو را به هم وصل می‌کند فقط کمی بیشتر از 180 درجه است، زیرا سطح این مثلث مساحت خیلی زیادی را روی زمین اشغال نمی‌کند و تقریباً صاف است.

به موجودات دو بعدی بازگردیم، آنها نیز می‌توانند از همین روش استفاده کنند و مشاهده کنند آیا فضای آنها خمیده است یا نه. آنها سوار بر سفینه‌های دو بعدی خود شده و از سیاره موطن خود بسوی یک ستاره دور دست پرواز می‌کنند، در آنجا به اندازه زاویه معینی مسیر خود را تغییر داده و بسوی ستاره دیگری حرکت خواهند کرد. هنگامی که به ستاره دوم رسیدند، سر سفینه را بسوی سیاره خود کرده و به آنجا باز خواهند گشت. اگر آنها مسیر حرکت خود را بررسی کنند و متوجه شوند که مجموع زوایای مثلث طی شده با 180 درجه فرق دارد [15] آنگاه به این نتیجه خواهند رسید که فضای آنها خمیده است.

مورد دیگری که ممکن است شما از دوران مدرسه بخاطر داشته باشید این ‌است که محیط یک دایره از ضرب عدد پی (π) در قطر آن بدست می‌آید. به ما گفته شده است که مقدار عدد پی، قابل بحث نیست و یک عدد ثابت است. دکمه‌ای روی اکثر ماشین‌های حساب قرار دارد که با فشردن آن، تا ده رقم اعشار این عدد نشان داده می‌شود (3.1415926536) ولی بیشتر ما فقط آن را 3 ممیز 14 صدم می‌شنایم. بسیار خوب، من اعتراف میکنم که به اندازه‌ یک ماشین حساب (ده رقم اعشار) این عدد را حفظ هستم، ولی دلیل آن اینست که من در کارم با این عدد خیلی سرو کار دارم، و حفظ کردن آن برایم از حفظ کردن یک شماره تلفن مشکلتر نیست. ولی ریاضی‌دانی را می‌شناسم که این عدد را تا سی رقم حفظ است، و تازه آن هم غیر طبیعی نیست. بگذریم، به ما یاد داده شده که عدد پی چیزیست که به آن یک ثابت ریاضی می‌گویند. تعریف این عدد عبارت است از : حاصل تقسیم محیط هر دایره‌ به قطر آن، بشرطی‌که آن دایره در فضایی بدون ‌انحناء قرار داشته باشد. اگر جهانگرد ما در طول مدار شمالگان [16] حرکت کند و قطر این مدار را با دقت اندازه بگیرد (این قطر برابر است با دو برابر فاصله مدار-شمالگان تا قطب شمال) و سپس آن را در عدد پی ضرب کند، او در خواهد یافت که عدد حاصل کمی از محیط مدار بیشتر است. انحناء زمین باعث شده که محیط این مدار از حالتی که زمین مسطح است، کوچکتر باشد.

این خواص مثلث‌ها و دایره‌ها که در مدرسه یادمی‌گیریم به هندسه اقلیدسی یا «هندسه-تخت» مشهور است. هندسه سه-بعدی کره، مکعب، استوانه و منشور نیز، اگر در یک فضای سه-بعدی مسطح و بدون انحناء قرار گرفته باشند، بخشی از هندسه اقلیدسی است. خواص این اشکال، هنگامی که فضای سه-بعدی دربردارنده آنها خمیده شود، تغییر خواهد کرد، همانطور که خواص مثلث و دایره وقتی بر سطح یک فضای خمیده دو-بعدی، مانند سطح کره، رسم شود تغییر می‌کند. بنابراین فضای سه-بعدی ما ممکن است خمیده باشد، ولی نیازی نیست برای دیدن این انحناء، ما یک فضای چهار-بعدی را مجسم کنیم. ما می‌توانیم با مطالعه هندسه اجسام سه-بعدی و حجم‌دار که در این فضا واقع شده‌اند، غیرمستقیم این انحناء را اندازه بگیریم. در حقیقت ما چیزی را ندیده‌ایم که برخلاف هندسه اقلیدسی باشد، زیرا در این قسمت از جهان هستی که ما قرار داریم، جهان تقریباً چنان مسطح است که ما نمی‌توانیم انحنایی را در آن مشاهده کنیم. این درست شبیه اینست که ما بخواهیم انحناء کره زمین را با رسم یک مثلث روی یک زمین فوتبال مشاهده کنیم. البته با مطالعه بسیار دقیق ما حتی می‌توانیم انحناء بسیار جزئی یک زمین فوتبال را هم اندازه بگیریم. به‌همین ترتیب، فضای سه-بعدی ما نیز در بعضی نواحی دارای انحناء است که در فصل بعدی به آن می‌پردازیم.

ولی اگر بعُد چهارمی در فراسوی فضای سه-بعدی ما قرار داشت آن وقت چه؟ ما در مورد خواص این فضا چه می‌توانیم بگوییم؟ بهترین راه برای شروع این ‌است که بپذیریم که فضای چهار بعدی برای موجودات سه-بعدی مثل ما، همان است که فضای سه-بعدی برای موجودات دو-بعدی. تصور کنید که شما در مرکز یک دایره بزرگ که برروی یک زمین صاف کشیده شده، مثلاً وسط استادیوم ورزشی، ایستاده‌اید. شما به هر طرف مستقیم قدم بردارید نهایتاً به پیرامون این دایره خواهید رسید. این جهت، جهت شعاعی[17] نامیده می‌شود، چون هنگامی که شما به پیرامون دایره رسیدید در حقیقت در طول شعاع دایره حرکت کرده‌ید. از سوی دیگر پرنده‌ای که وسط این دایره نشسته باشد می‌تواند در جهت بعد-سوم (یعنی بالا) حرکت کند. اگر او مستقیم به بالا پرواز کند درآنصورت همیشه از کلیه قسمتهای دایره دور خواهد شد.

حال یک بُعد دیگر به این مثال اضافه کنید و تصور کنید که پرنده‌ای در وسط یک کُره (مثلاً یک قفس کروی) نشسته است. حال این پرنده به هر طرف که پرواز کند، در جهت برخورد با پیرامون این کره (در حقیقت میله‌های قفس) خواهد بود، و تمام جهات برای او شعاعی خواهند بود. همانگونه که در مثال دو-بعدی پرنده می‌توانست از وسط دایره در طول بعد سوم بالا رود، حال ما می‌توانیم تصور کنیم که حرکت در بعد چهارم چه معنی می‌تواند داشته باشد؛ مسیر حرکت در بعد چهارم جهتی است که اگر پرنده‌ای که در وسط قفس قرار دارد در آن جهت حرکت کند، باید با ادامه این جهت از تمام نقاط داخل قفس فاصله بگیرد. این جهتی نیست که ما بتوانیم آن را تصور کنیم، زیرا همانطور که قبلاً اشاره کردم، مغز ما سه-بعدی است. بنابراین اگر ما یک پرنده جادویی داشته باشیم که در قفسی بدام افتاده و قادر باشد در جهتی در بعد چهارم حرکت کند ، ما از حرکت او چه خواهیم دید؟ ما خواهیم دید که او ناگهان از دید ما ناپدید می‌شود و در جای دیگری در فضای سه-بعدی ما، احتمالاً خارج از قفس، دوباره پدیدار می‌گردد. این برای ما همانقدر حیرت‌آور خواهد بود، که مهارت انجام جابجایی اشیاء توسط ما برای موجودات دو-بعدی.

اثر جالب توجه دیگری که استفاده از ابعاد بالاتر به بار می‌آورد آن چیزیست که هنگام برگرداندن اشیاء حاصل می‌شود. تصور کنید که شما قادرید یک موجود دو-بعدی را از جهانَش بلند کنید، و او را طوری برگردانید که سمت راست بدنش درسمت چپ قرار گیرد، و سمت چپ آن در سمت راست، آنگاه دوباره او را به جای اولش بازگردانید. تا مدتی، برای او چیزها حالت غریبی خواهند داشت. او چیز متفاوتی را احساس نمی‌کند، ولی برای او تمام اشیاء در جهت متضادی قرار گرفته‌اند. حالا برای او خورشید دو-بعدی‌، مانند قبل از سمت راست طلوع نمی‌کند، بلکه از سمت چپ طلوع خواهد کرد، و برای رسیدن بر سر کار نیز باید در جهت مخالفی از خانه حرکت کند.

اگر یک موجود چهار-بعدی شما را از دنیای سه-بعدی خود بلند کرده و سپس در فضای چهار-بعدی بچرخاند و دوباره به جای اول بازگرداند، دراینجا نیز چیزها برای شما حالت بامزه‌ای خواهند داشت. نخست، دیگران متوجه تغییر کوچکی در ظاهر شما می‌شوند، چون بنظر آنها صورت کنونی شما مانند آن است که قبلاً در آینه دیده می‌شد. شما هم بار دیگری که به آینه نگاه کنید چهره‌ای متفاوت از آنچه قبلاً می‌دیدید مشاهده خواهید کرد. دلیل این امر این است که چهره هیچ کس متقارن نیست. سمت چپ صورت ما با سمت راست متفاوت است، ممکن است یک اَبرو کمی بالاتر از دیگری باشد و یا، مثل من، نوک بینی به یک سمت متمایل باشد، و یا در یکی از گونه‌ها چالی باشد و غیره. ولی این تازه اول مشکلات است؛ همه چیز در اطراف شما عقب-جلو بنظر میرسد، عقربه‌های ساعت در جهت عکس حرکت می‌کنند، تمام نوشته‌ها در جهت معکوس نوشته شده‌اند و شما اگر قبلاً راست-دست بوده‌اید حالا چپ-دست شده‌اید. تنها راه برای اینکه دنیا را مثل قبل ببینید این است که همه چیزا را از درون یک آینه نگاه کنید. مدتی طول خواهد کشید تا شما دیگر به چیزهای اطراف خود تنه نزنید.

آیا واقعاً بُعد چهارمی در کار هست؟

اگر شما چیزی در مورد نظریه نسبیت اینشتین بدانید (که من فرض می‌کنم نمی‌دانید) ممکن است در این مرحله کمی نگران شوید. مگر اینشتین نگفته بود که بعد چهارم همان زمان است؟ من در فصل 6، نظریه نسبیت را مورد بحث قرار خواهم داد و در آنجا خواهیم دید که چگونه فضا و زمان بصورت حیرت آوری باهم مرتبط هستند، و چیزی به نام فضا-زمان چهار-بعدی را بوجود می‌آورند. فعلاً ما می‌توانیم برای روشن شدن این مطلب، مثال ساده زیر بیاوریم؛ به مورد زیر دریایی باز میگردیم که برای مشخص شدن موقعیت خود به سه عدد نیاز داشت. اگر زیر دریایی در حال حرکت باشد، گفتن این سه عدد معنایی نخواهد داشت، مگراینکه بگوییم زیر دریایی در چه زمانی در این موقعیت بوده. بنابراین حالا ما به چهار عدد برای مشخص کردن موقعیت زیردریایی نیاز داریم: طول جغرافیایی، عرض جغرافیایی، عمق (فاصله از سطح آب) و همچنین زمانی که در این مختصات قرار داشته است. ولی ما نباید این واقعیت را فراموش کنیم که زمان با سه بعد فضایی دیگر متفاوت است. ما آزادیم که در طول هریک از محورهای فضایی به عقب وجلو حرکت کنیم، ولی در طول محور زمان مُقید هستیم که فقط به جلو حرکت کنیم (از حال به سوی آینده). سئوال این است که آیا فراتر از حواس ما، یک بعد چهارم فضایی، می‌تواند وجود داشته باشد.

حدود یکصد سال قبل، برخی از محترم‌ترین دانشمندان جهان، به دنیای اشباح، جایی که قلمرو ارواح و اجنه است، می‌گفتند بعد-چهارم، و فکر می‌کردند که جهان سه-بعدی ما در داخل چنین جهانی قرار دارد. ساکنان این جهان چهار-بعدی، گاه‌ و بیگاه از دنیای ما عبور می‌کردند، ولی بیشتر اوقات بر ما پنهان بودند. البته این روزها، بسختی می‌توان یک دانشمند واقعی پیدا کرد که به این مسائل اعتقاد داشته باشد (البته غیر از دانشمندنماهای دیوانه). این‌مورد به این معنی نیست که ابعاد بالاتر نمی‌توانند وجود داشته باشند. در حقیقت، بعضی از جدیدترین نظریات در فیزیک مدرن (که هنوز مورد آزمایش و تائید قرار نگرفته‌اند)، ایجاب می‌کنند که حتی ممکن است بیشتر از چهار بعد فضایی موجود باشد، و تمام این ابعاد اضافی خارج از فهم ما قرار دارند. دو نظریه مهم دراین‌مورد، که یکی به نظریه ابر-ریسمان‌ها [18] ودیگری به نظریه اِم [19] (M) شهرت دارند، حاکی از این هستند که جهان ما درواقع دارای 9 یا 10 بعدی فضایی و یک بعد زمانی است [20]. ولی بقیه ابعاد اضافه چنان بصورت تا- خورده‌ و کوچک درآمده‌اند، که ما هرگز قادر به آشکار سازی آنها نخواهیم بود. ممکن است شما اینها را بعنوان سخنان بی‌مزه قلمداد کنید، ولی واقعیت این ‌است که یکی از این دو نظریه عجیب می‌تواند (فعلاً معلوم نیست کدام) توصیفی نهایی از واقعیت‌های بنیادی جهان ما باشد.

همانطور که در فصل‌های بعدی خواهیم دید، حتی اگر فضا، همان فضای سه-بعُدی باشد که همه ما می‌شناسیم، مفید است تا برای شناخت بهتر بعضی از جنبه‌های نظریه نسبیت اینشتین (یعنی خمیدگی فضا)، یک بعد اضافه در آستین خود آماده بکار داشته باشیم.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 2

اهمیت گرانش

$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image001.jpg$

سیب‌ و ماه‌

در افسانه‌ها آمده است که روزی آیزِک نیوتون [21] زیر درختی نشسته بود و ناگهان از بالای درختی سیبی بر سر او فرود می‌آید و همین امر موجب کشف قانون گرانش توسط او می‌شود (البته این امر می‌تواند دلالت بر این نیز داشته باشد که ضربه‌ای که بر سر او وارد شده، درست مانند فیلمهای کارتون، لامپی را بالای سر او روشن کرده و ناگهان جرقه‌ای را ذهن او بوجود آورده که «عجب!، بنظر می‌رسد زمین نیرویی را به این سیب وارد کرده و موجب افتادن آن شده.»). البته این مسئله به این سادگی هم که روایت کرده‌اند نیست. نیوتون اولین کسی نبود که متوجه شد چیزها به زمین سقوط می‌کنند! بصیرت او فراتر از این بوده است.

خوب، این مسئله افتادن سیب به سر نیوتون ممکن است افسانه باشد، ولی برطبق روایاتی که از خود نیوتون نقل می‌کنند، او روزی در مزرعه مادرش در اندیشه افتادن سیب (و بسیاری از مسائل دیگر از قبیل اینکه چرا ماه به دور زمین می‌گردد) بود، و این فکر موجب هدایت او به سمت قانون معروف گرانش عمومی شد. چه چیز عجیبی در مورد افتادن سیب وجود داشت که دیگران نتوانسته بودند به آن پی ببرند؟ اگر بطور ساده بیان کنیم، او چیزی را دیده بود که بر دیگران آشکار نبود؛ اینکه تمام اشیاء تمایل دارند به درون زمین حرکت کنند و اینکه نه فقط سیب برروی زمین، بلکه زمین هم برروی سیب سقوط می‌کند. در حقیقت بهتر است دیگر از این پدیده به نام «افتادن و سقوط» نام نبریم بلکه بگوییم سیب و زمین بسوی یکدیگر جذب می‌شوند.

مرد خانواده‌دار، معاشرتی و محبوب. هیچ یک از این صفات در مورد نیوتون صدق نمی‌کرد. اوکه در شهر وُل‌استروپ [22] در استان لینکلن‌شایر [23] انگلستان در شب کریسمس سال 1642 بدنیا آمد، آدم گوشه‌گیری بود که هرگز ازدواج نکرد و دوستان زیادی نیز نداشت. در مقابل، بعداً در آواخر عمرش، بر سر اینکه چه کسی زودتر چه اکتشافاتی را انجام داده، درگیر نزاعی طولانی با بقیه دانشمندان هم عصر خود شد. ولی، برخلاف تصویر منفی که امروز در رسانه‌های عامه پسند از دانشمندان نشان داده می‌شود، و باعث شده بسیاری از نوجوانان از این موضوعات دور بمانند، حقیقتاً نیوتون یک دانشمند معمولی نبود. آنچه که او در آداب و معاشرتهای اجتماعی کم داشت در جای دیگری جبران شده بود تا، به نظر عده کثیری، از او بزرگترین دانشمند تاریخ را بسازد. او چنان دستاوردهای عظیمی در حوزه‌های مختلف علم از خود بجا گذاشت که اکنون قسمت مهمی از آنچه در دبیرستان به نام فیزیک تدریس می‌گردد، ازآن به نام فیزیک نیوتونی نام می‌برند. و البته این متفاوت است با مبحثی که فیزیک مدرن قرن بیستم نامیده می‌شود و در این کتاب مورد بررسی قرار می‌گیرد. نیوتون همچنین حساب دیفرانسیل و انتگرال (حسابان) را، که ابزارهای اصلی برای مطالعه علوم امروز هستند، اختراع کرد. ولی کشف حساب دیفرانسیل و انتگرال موجب بوجود آمدن یک جدال طولانی شد. موضوع اختلاف این بود که آیا نیوتون زودتر آن را کشف کرده بود و یا فیلسوف و ریاضیدان آلمانی گوتفرید لِیب‌نیتز [24]. در حلقه دانشمندان آن روز، نزاع بر سر اینکه آیا این انگلیسی‌ها بودند که این ایده را از آلمان‌ها دزدیده‌اند و یا بلعکس، موجب بوجود آمدن یک حس میهن پرستی شده بود، که تاکنون نیز خود را در قالب رقابتهای فوتبال نشان می‌دهد. ولی برخلاف امروز که تکلیف نهائی دو تیم مساوی را با ضربات پنالتی مشخص می‌کنند، در نبرد حساب دیفرانسیل و انتگرال هیچ برنده‌ای در کار نبود. بنظر می‌رسد که هر دو در یک زمان، بطور مستقل از یکدیگر، آن را کشف کرده‌ بودند. در هرحال، بیشتر کارهای اساسی حدود نیم قرن قبل از آنها توسط ریاضیدان بزرگ فرانسوی پی‌یر فُرما انجام گرفته بود!

به گرانش بازگردیم. مدتها پیش از نیوتون، معلوم شده بود آنچه که باعث می‌شود اشیاء سقوط کنند این ‌است که زمین نیروئی را بر آنها اعمال می‌کند و باعث می‌شود به طرف پائین کشیده شوند. همچنین مشخص بود که ماه نیز به این‌دلیل به دور زمین می‌گردد که زمین نیروی مرموزی را بر آن اعمال می‌کند و آن را وادار می‌کند که در فضا سرگردان نشود. نیوتون رابطه‌ای مابین این دو پدیده پیدا کرد. نسبت دادن حرکت ماه و سیبِ درحالِ سقوط به یک نیرو (گرانش)، حاصل نبوغی متهورانه بود. تا قبل از آن تصور می‌شد دو نیروی جداگانه بر این دو قلمرو زمینی (یعنی سیب) و آسمانی (ماه) حکمفرماست.

قانون گرانش نیوتون می‌گوید که هر دو جسمی در جهان، توسط نیرویی نامرئی جذب یکدیگر می‌شوند. زمین وکلیه اجسام روی آن، ماه و زمین، خورشید و کلیه سیارات اطراف آن، حتی خورشید و بقیه ستارگان موجود در کهکشان ما، همه بسوی یکدیگر کشیده می‌شوند. پس این تنها زمین نیست که ما را به سطح خود چسبانده، بلکه بعبارتی ما نیز زمین را به پاهای خودمان چسبانده‌ایم، زیرا همانقدر که زمین نیروئی را برما اعمال می‌کند ما نیز به همان اندازه آن نیرو را بر زمین اعمال می‌کنیم. وقتی پیش ازاین گفتم زمین نیز به طرف سیب، به بالا سقوط می‌کند، این حرف کاملاً جدی بود. دقیقاً همین‌گونه است، ولی چون ما به زمین چسبیده‌ایم، می‌بینیم که سیب بطرف زمین حرکت می‌کند. ولی سیب نیز حق دارد ادعا کند که این او نیست که سقوط می‌کند بلکه زمین است که بطرف او می‌آید (البته این ادعا به همان اندازه قد وقامت سیب نسبت به زمین ارزش دارد!).

به همان وجه، یک مرد و زن سرگردان در فضا نیز، بطور فیزیکی جذب یکدیگر می‌شوند، حتی اگر بطور فیزیکی [25] برای یکدیگر جاذبه‌ای نداشته باشند! (بوسیله نیروی گرانشی که باعث می‌شود به آهستگی بسوی یکدیگر جذب شوند). ولی این نیرو بسیار ضعیف است. (اگر فاصله آنها چند سانتیمتر باشد، آنگاه این نیرو به اندازه نیروئی است که برای برداشتن یک دانه شکر لازم است). نیروی گرانش وقتی جرم اجسام درگیر کم باشد، بسیار ضعیف است.

چطور این نیروئی که موجب میشود تا سیب سقوط کند، موجب نمی‌شود تا ماه نیز بطرف زمین کشیده شود. تفاوت این دو حالت در اینجاست که ماه، علی‌رقم جرم بیشترش، در مداری بدور زمین می‌گردد و در هر لحظه در جهتی حرکت می‌کند که با شیب خط مماس بر مدارش برابر است، در صورتیکه سیب بطرف مرکز زمین حرکت می‌کند. درواقع این راه خوبی برای توصیف این پدیده نیست. بهتر است بجای گفتن اینکه «در مداری بدور زمین می‌گردد» بگوئیم که ماه نیز همچون سیب بر روی زمین سقوط می‌کند ولی مسیر سقوط آن یک منحنی به شکل دایره است، بنابراین هرگز نمی‌تواند به زمین نزدیکتر شود. هنگامیکه نیوتون نخستین بار، در طی سال 1666 که انگلستان در گیر طاعون بود، این مسئله را مورد محاسبه قرار داد، او پیش خود فکر کرد که جوابی اشتباه بدست آورده و ناامیدانه از انتشار آن خودداری کرد. فقط در سالها بعد، در زمانیکه با دوستش ادموند هالی (کسی که ستاره دنباله دار معروف به نام اوست) مسئله را مورد بررسی قرار داد، او پی به اهمیت کشف نیوتون برد.

قانون گرانش نیوتون بطور شگرفی در طول سیصد سال موفق بود. توجه داشته باشید دانشمندان به آن نام قانون داده بودند، زیرا چنان مطمئن بودند که در این موضوعات حرف آخر را می‌زند که آن را از جایگاه یک نظریه محض،که بعداً می‌توانست توسط شخصِ دیگری رد شود، به قانون ارتقاء دادند. ولی این دقیقاً همان چیزی بود که در سال 1915 اتفاق افتاد. آن شخص اینشتین بود، آلبرت اینشتین.

گرانش اینشتین

بنظر میرسد قانون گرانش نیوتون می‌تواند این نیروی نامرئی و تقریباً سحرآمیز را که میان اجسام اعمال می‌شود توصیف کند. مهم نیست این اجسام چقدر از هم دور هستند (البته با زیاد شدن فاصله مقدار آن ضعیف‌تر می‌شود) و یا در میان آنها چه چیزی وجود دارد؛ حتی میان آنها می‌تواند فضای خالی باشد. بنابراین، ما می‌گوییم که نیروی گرانش به یک میانجی (یا واسط) برای اعمال شدن نیاز ندارد. اینشتین توصیفی عمیقتر از این می‌دهد. او ادعا می‌کند که گرانش مستقیماً بر اجسام اثر نمی‌کند، بلکه بر فضا تاثیر می‌گذارد و موجب خمیدگی آن می‌شود. این خمیدگی یا انحناء فضا موجب می‌شود تا اجسام موجود در آن، بصورتی متفاوت نسبت به زمانی که این انحناء وجود ندارد، رفتار کنند. گیج شده‌اید؟ بیائید به عقب بازگردیم و ببینیم چگونه اینشتین به این تفسیر پیچیده و غیرضروری رسید.

آیا تابحال به آن اطاقکهائی که در پارکهای تفریحی قرار دارد و تعقیب‌ و گریز‌های پرهیجان را برای شما شبیه ‌سازی می‌کند رفته‌اید؟ در آنجا شما بهمراه چند نفر در یک کپسولِ دربسته قرار می‌گیرید و در جلو شما یک فیلم تعقیب و گریز به‌نمایش درمی‌آید. شما احساس می‌کنید که این کپسول است که واقعاً حرکت می‌کند، شتاب می‌گیرد، ترمز می‌کند، درسر پیچ‌ها قژقژ می‌کند، در دست‌آندازها تکان‌ می‌خورد، بالا میرود و پائین می‌آید. در حقیقت، خیلی ساده می‌توان شما را فریب داد. اصلی که در این دستگاه‌ها بکار گرفته میشود به اصل هم‌ارزی اینشتین معروف است و چنان ساده است که می‌توان آن را در یک کلمه بیان کرد: نیروی-گرانش (دو کلمه بود یا یکی!؟) اینشتین دریافته بود که نیرویی که شما موقع شتاب گرفتن احساس می‌کنید (مثلاً هنگامیکه در هواپیما هستید، و هواپیما برای بلند شدن روی باند فرودگاه سرعت می‌گیرد) و نیروی گرانش با هم یکی هستند. در حقیقت، ما می‌گوئیم که شتابی که در هواپیما ما را به سمت صندلی می‌کشد، با شتابی که اجسام هنگام سقوط می‌گیرند هر دو از یک جنس‌ هستند.

در نظر اول این کمی بعید بنظر می‌رسد، چون به هرصورت نیروئی که شما را در صندلی به عقب می‌کشد، بواسطه حرکت شتابدار است، در حالی که نیروی گرانش هنگامی عمل می‌کند که شما درجای خود ساکن ایستاده‌اید (با کشیدن شما به طرف زمین). ولی کمی در مورد طرز کار این‌ اطاقک شبیه‌ساز فکر کنید؛ چگونه است که حتی وقتی شما چشمان خود را بروی آن تصویر گول‌زننده می‌بندید، باز هم احساس شتاب می‌کنید؟ درهرحال، این اطاقک به هیچ‌جایی حرکت نمی‌کند و تنها درجای خود، یا تکان می‌خورد و یا کج می‌شود. تنها کاری که این دستگاه باید انجام دهد تا شما را قانع کند که درحال شتاب گرفتن به جلوست، این ‌است که طوری بچرخد که سر شما به سمت بالا قرار گیر و فشار نیروی جاذبه موجب شود تا به صندلی خود فشرده شوید، و این درست همان احساسی است که در حرکت شتابدار ماشین و یا هواپیما به شما دست می‌دهد. ما چنان به این حس عادت کرده‌ایم که وقتی هنگام شب، سر خود را بر بالش می‌گذاریم، فراموش می‌کنیم که این نیروی جاذبه است که سر ما را بر بالش فشار می‌دهد. در حقیقت این نیروئی که ما آن را عادی فرض می‌کنیم، از نظر مقدار همان قدر به سر شما فشار وارد می‌کند، که به پشتی صندلی شما درهنگام نشستن در ماشینی که شتاب آن چنان است که در مدت زمان دو ونیم ثانیه به سرعت صد کیلومتر در ساعت برسد!

درست به همین دلیل، فریب دادن مغز تا این حد ساده است که ما نیروی جاذبه در آن اطاقک را با نیروی حرکت شتابدار اشتباه می‌گیریم. به همین ترتیب هنگامیکه این شبیه‌ساز روبه پائین قرار دارد و ناگهان متوقف می‌شود، ما که بجلو خم شده‌ایم تصور می‌کنیم که ماشین ترمز گرفته!

مثال دیگری که اصل هم‌ارزی را در عمل نشان میدهد حالت عکس مثال قبل است، یعنی استفاده از شتاب برای شبیه سازی گرانش. مثال معمول برای توضیح این مسئاله بصورت زیر است: فرض کنید درحالی که کمربند ایمنی خود را بسته‌اید، در سفینه‌ای که آماده پرواز است در صندلی خود نشسته‌اید. صندلی شما چنان است که صورتتان روبه بالا قرار دارد (به طرف نوک سفینه‌) و شما به صندلی خود فشرده ‌شده ‌اید. بعلاوه تصور کنید چنان احساس آسودگی می‌کنید که همانطورکه در حالت طاق‌باز قرار دارید به خوابی عمیق فرو رفته‌اید (بله می‌دانم، چنین چیزی کمتر اتفاق می‌افتد). هنگامیکه شما از خواب بیدار می‌شوید، و قبل از اینکه فرصت کنید از پنجره بیرون را تماشا کنید، اصل هم‌ارزی می‌گوید که شما قادر نیستید تشخیص دهید که آیا هنوز در حال طاق‌باز منتظر پرتاب سفینه‌ هستید و یا اینکه با شتابی ثابت برابر با شتاب جاذبه زمین در حال دور شدن از زمین می‌باشید. در حقیقت اگر شما از نگاه کردن به بیرون پنجره پرهیز کنید، برای اینکه ببینید هنوز در سکوی پرتاب منتظر پرواز نشسته‌اید و یا اینکه در فضای بالای زمین قراردارید، هیچ آزمایشی نیست که شما بتوانید در درون سفینه‌ انجام دهید تا به درستی قادر به تشخیص این دو حالت از یکدیگر شوید [26]. منظور من از آزمایش، شامل هر مشاهده ساده‌ای مانند نوسان یک پاندول، سقوط یک توپ یا اندازه‌گیری‌های دقیقتر با استفاده از آینه و پرتو لیزر، می‌شود؛ و اساساً هر آزمایشی که بتواند در رفتار یک جسم هنگامی که تحت تاثیر گرانش است، و یا با شتابی به اندازه شتاب جاذبه زمین حرکت می‌کند، تمایزی قائل شود.

سرانجام، تردید باعث می‌شود تا روی خود را بطرف پنجره بگردانید و مشاهده کنید که حقیقتاً شما در حال شتاب گرفتن در فضا هستید. ولی چون آنهمه آزمایش فیزیک شما را خسته کرده، به جای خود بازمی‌گردید و دوباره بخواب می‌روید! هنگامی که از خواب بیدار می‌شوید احساس بی‌وزنی می‌کنید. خوشحال می‌شوید که فراموش نکرده بودید کمربند ایمنی خود را ببندید، چون دراینصورت ممکن بود در حال بی‌وزنی سرتان به دستگاه‌های اطراف بخورد. حالا اگر شما به بیرون از پنجره نگاه نکنید با معمای دیگری دست‌بگریبان هستید. دراین‌حالت دلیل بی‌وزنی شما، یا می‌توانید این باشد که همانطورکه موتور سفینه‌ خاموش شده، در فضا شناور مانده‌اید، ویا می‌تواند از سقوط شما به داخل اتمسفر زمین باشد، که دراینصورت بطور جدی خطر مرگ شما را تهدید می‌کند و باید هر چه سریعتر کنترل سفینه‌ را بدست بگیرید. پس می‌بینید هنگامیکه شما بطور آزاد در حوزه گرانش زمین سقوط می‌کنید، چنان احساس بی‌وزنی دارید، که انگار جاذبه زمین قطع شده است و شما در فضای بیرون از زمین قرار دارید.

سقوط آزاد

بیشتر ما شانس این را نداریم تا در موقعیتی که قبلاً به آن اشاره شد قرار بگیریم، بنابراین برای روشن مطلب مثال دیگری را می‌آورم.

نمی‌دانم هرگز شهامت (یا حماقت؟) آن را داشته‌اید که از بالای یک پل بلند که بر روی یک رودخانه قرار دارد، و با طنابی کش‌دار که شما را به پل متصل می‌کند، به پائین بپرید [27] یا نه. اگر اینکار را کرده‌ باشید آنگاه همانطور که بصورت مستقیم در حال سقوط هستید، احساس خواهید کرد که در هیچ زمانی کششِ جاذبه‌زمین خود را به این صورت مهیج نمودار نکرده است. ولی در واقع درست برخلاف این اتفاق می‌افتد. ممکن است برای اولین‌ بار باشد که فکر کنید عمل گرانش کاملاً متوقف شده و باصطلاح گفته می‌شود شما درحال «سقوط آزاد» هستید. در آن لحظات نشاط‌آور، شما شاهد جاذبه صفر هستید. به هر حال گرانش همیشه تاثیر خود را خواهد داشت و همان‌کاری را انجام می‌دهد که در تمام طول عمر شما انجام داده، فقط تنها چیزی که در این حالت غایب است، آن زمین محکمی است که همیشه زیر پای شما قرار داشته. بنابراین، گرانش کارش را تمام کرده، و موقتاً، تاوقتی که شما قدم به زمین بگذارید، غایب است. به عبارت بهتر، بجای اینکه بگوئیم گرانش غایب است، بهتر است بگوئیم گرانش در مقابل شتابی که شما گرفته‌اید بکلی خنثی شده. حس سقوط آزاد آن چیزیست که فضانوردان هنگامی که در فضا، و به دور از گرانش زمین به‌ سر می‌برند احساس می‌کنند. تعجب‌آور نیست که آنها برای چیره‌شدن بر حالت تهوع در فضا، متحمل تمرین‌های زیادی می‌شوند، و اگر بگوئیم «سفر فضائی مانند یک پرش از پُلِ دراز مدت است»، این گفته نادرست نیست.

جاذبه صفر یعنی چه؟ فرض کنید همانطور که شما در حال سقوط هستید، سنگی را که در دست دارید رها می‌کنید. بدلیل اینکه سنگ نیز با همان سرعتی که شما حرکت می‌کنید، درحال حرکت است، در نتیجه درکنار شما خواهد بود. حالا بنظر می‌رسد که سنگ در کنار شما معلق مانده، درست به همان‌صورتیکه اشیاء در جاذبه صفر در فضا معلق می‌مانند. به همین دلیل است که شما در مورد سفینه، بدون نگاه کردن به بیرون، قادر نبودید بگوئید که آیا سفینه در آتمسفر زمین سقوط می‌کند، یا اینکه در فضای بالای زمین شناور مانده است.

مثالهائی از این نوع که من شرح دادم به آزمایش‌های فکری معروف هستند، زیرا برای بدست آوردن نتایج این آزمایش‌ها، نیازی به انجام عینی آنها نیست. اینشتین یکی از طرفدارن پر وپا قرص چنین رویکردهایی بود، زیرا او بیشتر وقت خود را به نشستن و فکر کردن می‌گذراند، تا کار در آزمایشگاه و انجام آزمایش‌های واقعی. او به این‌نوع آزمایش‌ها، گِدآن‌کِن می‌گفت ('gedanken' در زبان آلمانی یعنی فکر کردن). البته پرش از پُل و اطاقک‌های شبیه‌ساز حرکت شتابدار که در آنها فیلم به‌نمایش درمی‌آید، جزء مثال‌ها و آزمایش‌های ‌فکری او نبود.

همه این مسائلی که در مورد شتاب گفتیم چه ارتباطی با نظر اینشتین درباره خمیدگی فضا دارد؟ متاسفم که برای روشن شدن این مطلب، مجبورم کمی بیشتر توضیح بدهم. باید به مثال سفینه بازگردیم؛ یعنی همان قسمتی را که تازه از خواب بیدار شده بودید و نمی‌توانستید، بدون نگاه کردن به بیرون، مشخص کنید که آیا سفینه هنوز درسکوی پرتاب است و یا باشتابی برابر جاذبه زمین درحال حرکت کردن در فضا است. دراینجا یک آزمایش فکری ویژه وجود دارد که شما باید انجام دهید. در یک طرف سفینه بایستید و یک توپ را بصورت افقی به سمت دیگر پرتاب کنید (شکل 2.1a). توپ مسیری منحنی را طی خواهد کرد، و کمی پایینتر از مسیر مستقیم، بطرف دیگر سفینه برخورد می‌کند. این درست همان چیزی است که ما انتظار داریم هنگامی که سفینه بدون حرکت روی سکوی پرتاب قرار دارد، اتفاق بیفتد: یعنی پیروی توپ از قانون گرانش و حرکت بصورت منحنی.

حال اگر سفینه در فضا باشد و شتاب بگیرد، شما باید طبق اصل هم‌ارزی، مسیرِ منحنیِ مشابه‌ا‌ی را ببینید. اگر موتورهای سفینه خاموش شوند و سفینه در فضا شناور شود (با سرعت ثابتی حرکت کند) و آزمایش با توپ تکرار شود، آنگاه خواهید دید که توپ یک مسیر مستقیم را طی خواهد کرد. این به ‌این‌دلیل است که توپ و سفینه هر دو دارای یک حرکت «روبه ‌بالا» هستند. ولی اگر در زمان پرتاب توپ، سفینه ناگهان شتاب بگیرد (شکل 2.1b)، آنگاه هنگامی که توپ در میان راه است، این شتاب را حس نخواهید کرد (توجه داشته باشید که دو شکل قسمت b یک چیز را نشان میدهد: شکل سمت راست، کسری از ثانیه بعد از شکل سمت چپ است). بنابراین هنگامی که توپ به سمت دیگر می‌رسد، خود سفینه چون سریعتر از توپ حرکت کرده در فاصله بالاتری قرار خواهد داشت، و چون دیوار مقابل هم بالا رفته، درنتیجه نقطه برخورد توپ کمی پائینتر از مسیر مستقیم خواهد بود، و بنظر شما اینطور می‌رسد که توپ یک مسیر منحنی را طی کرده. اصل هم‌ارزی در اینجا نیز درست است. اگرچه توصیف مسیر منحنی در دوحالت متفاوت است، ولی تاثیری را که شما مشاهده می‌کنید، در هر دو حالت یکی است.

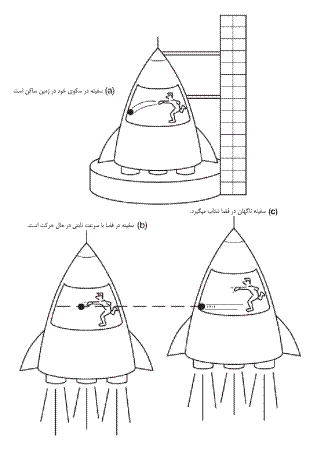
$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image010.gif$

شکل 2.1- (a) توپ پرتاب‌ شده‌ای که تحت تاثیر گرانش زمین قرار دارد، یک مسیر منحنی را طی خواهد کرد. (b) توپ پرتاب شده‌ای که تحت گرانش صفر یک حرکت مستقیم‌الخط را دارد، با روشن شدن موتور سفینه و شتاب گرفتن آن، یک مسیر منحنی را طی خواهد کرد، زیرا سفینه تا زمانی که توپ بخواهد به آن سوی سفینه برسد، بالاتر خواهد بود.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 3

جهان

$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image001.jpg$

جهان ممکن است بسته باشد، ولی پس از صرف ناهار دوباره باز خواهد شد!

اِریکا تورستون، دانشجوی دانشگاه سُری

آسمان شب

در صورتیکه شما هم مثل من‌ در نواحی پر جمعیت شهری زندگی ‌کنید، جاهایی که حتی در یک شب صاف نیز آسمان چنان کدر است که تنها می‌توان اجسام خیلی درخشان را مشاهده کرد، آنگاه تشخیص بسیاری از ستارگان و سیارات کار بسیار مشکلی خواهد بود. من می‌توانم به غیر از ماه، نزدیکترین همسایگانمان، یعنی مریخ و زهره، را تشخیص دهم، ولی دیگر نمی‌شود در مورد صورتهای فلکی مطمئن بود. در سنین کودکی با آسمان شب مانوس‌تر بودم.

من در بغداد بدنیا آمدم، و شانزده سال اول زندگیم را در آنجا گذراندم. ولی هنگامیکه در اواخر دهه 1970 اوضاع سیاسی تغییر کرد، بمنظور زندگی بهتر، بهمراه خانواده‌ام عراق را ترک کردم. تا پیش از آن، هر چند سال یک بار تعطیلات تابستانی را در خانه پدربزرگم در انگلستان می‌گذراندیم. ولی شبهای تابستانِ عراق چیز دیگری بود. آخرین ابرهای بهاری در اوایل اردیبهشت ناپدید می‌شدند و تا اوایل آبان ماه آسمان بدون لکه باقی می‌ماند. تعطیلات تابستانی مدارس سه ماه و نیم طول می‌کشید. در طول ماه‌های تیر و مرداد دمای هوا به چهل‌وپنج درجه می‌رسید و شب‌ها بسختی به حدود سی درجه بازمی‌گشت.

یکی از مراسم هیجان‌انگیز در خاورمیانه که نوید آمدن تابستان را می‌داد پهن کردن رختخواب بر پشت‌بام‌ها بود. خانه‌ها دارای پله‌کانهایی بودند که به یک بام مسطح منتهی می‌شد و همه به مدت سه ماه برای فرار از گرما و رطوبت در آنجا می‌خوابیدند. بنابراین همیشه شبهای تابستان به این معنی بود که درحالی به آسمانی مملو از هزاران ستاره خیره شده‌ای، سعی کنی با متصل کردن آن نقاط نورانی به هم، در ذهن خود یک شکل بسازی. البته بخاطر پشه‌بندهایی که برای جلوگیری از مزاحمت حشرات روی رختخوابهای خود می‌بستیم تصویر آسمان تا اندازه‌ای کدر می‌شد. ولی درعوض کسی به فکر باران نبود، چون هیچگاه در تابستان باران نمی‌آمد.

حالا که در جنوب انگلستان زندگی می‌کنم تازه می‌فهمم که چقدر آسمان شب می‌تواند زیبا باشد، و بعضی اوقات دلم برای دیدن شهاب‌ها تنگ می‌شود.

بگذریم، داشتم می‌گفتم هنگامی که بچه بودم می‌توانستم تعدادی از ستارگان را از هم تشخیص دهم. در آن زمان من یادگرفته بودم که برخی از این درخشان‌ترین ستارگان درحقیقت ستاره نبودند، بلکه سیاراتی بودند که همچون ماه، نور باز تابیده شده از خورشید را منعکس می‌کردند. ستارگان واقعی میلیون‌ها بار دورتر از سیارات قرار داشتند، و بنابراین می‌بایست درخشندگی واقعی آنها چنان زیاد باشد که همچنان از این فاصله دور قابل مشاهده‌اند. همچنین خاطرم هست هنگامیکه فهمیدم یک شهاب چیزی نیست جز یک سنگ درحال سوختن که از جو زمین عبور می‌کند، هم ناامید شدم و هم خشنود.

مباحث مطرح شده در این بخش شامل دو حوزه کاملاً مرتبط به هم، یعنی ستاره شناسی و کیهان‌شناسی [28]، می‌شود. بسیاری از اشخاص تصور درستی از ستاره‌شناسی در ذهن دارند، درحالیکه در مورد کیهان‌شناسی اینطور نیست. از قسمت «شناسی» که بگذریم، روی هم رفته کیهان‌شناسی بنظر کلمه‌ای زیبا و تا حدی هیبت‌انگیز بنظر می‌رسد. این شاخه از علم، کل جهان هستی را مورد مطالعه قرار می‌دهد، چیزهایی از قبیل: اندازه و شکل جهان، تکوین و تکامل و حتی سرنوشت احتمالی آن. همچنین بنظر می‌رسد کیهان‌شناسی باشکوه‌ترین رشته فیزیک است. این حوزه به مسائلی توجه می‌کند، و حتی مدعای پاسخ‌گویی به چیزهایی است، که بسیاری معتقدند خارج از قلمرو فیزیک می‌باشد.

آنچه که ما در مورد جهان می‌دانیم بوسیله آزمایشات دقیق و طاقت‌فرسا و همچنین رصدهای نجومی حاصل شده که بطور پیوسته با ساخته شدن تلسکوپهای قویتر و کاربرد تکنیک‌های جدید در حال بهبود می‌باشد. اگرچه کیهان‌شناسی یکی از شاخه‌های ستاره‌شناسی است، ولی دانسته‌های ما در مورد جهان، از شاخه‌های دیگری همچون فیزیک هسته‌ای، فیزیک ذرّات بنیادی و فیزیک‌نظری نیز منشاء گرفته‌اند. کیهان‌شناسی-نظری، شامل ساختن مدل‌های ریاضی فرضی از جهان است که از حل کردن معادلات نسبیت عام اینشتین حاصل می‌شود. این معادلات بصورتی فرمول‌بندی می‌شوند تا نه فقط بتوان از آنها توصیفی از ویژگی‌های ناحیه‌ کوچکی از فضا و زمان در همسایگی یک جسم سنگین، مانند یک ستاره، بدست گرفت، بلکه می‌توانند توصیفی برای ویژگی‌های کل جهان نیز به ما بدهند.

در بخشهای دیگر در مورد ایده‌هایی، که حداقل در زمان نوشتن این کتاب مشخص کننده بهترین درک ما از جهان هستی هستند و همچنین نظریات مطرح در این زمینه، سخن خواهم گفت. ممکن است تا چند سال دیگر ثابت شود برخی از این نظریات اشتباه بوده‌اند. از سوی دیگر برخی ویژگی‌های خاص جهان هستند که ما در مورد آنها کاملاً اعتماد داریم، و من معتقد‌م در برابر آزمون زمان مقاوم خواهند بود. در پایان این فصل به ویژگی‌هایی که بنظر من صحیح هستند، و آنهایی که هنوز بر سر آنها بحث است، اشاره خواهم کرد.

بمنظور اینکه به شما نشان دهم با اندازه‌گیری‌های هرچه دقیقتر، تغییر نظریات در کیهان‌شناسی چقدر سریع صورت می‌گیرد، باید بگویم من در طول غلط‌گیری دستنویس این کتاب، مجبور شده‌ام تا قسمتهای مهمی از این فصل را چندین بار تغییر دهم و آنها را از نو بنویسم. در واقع همانطور که خواهیم دید سال 1998 سال مهمی برای کیهان‌شناسی بود.

جهان چقدر بزرگ است؟

در پاسخ این سئوال من همیشه میگویم «خیلی بزرگ!» و به همین بسنده می‌کنم. درحقیقت، بر طبق بسیاری از شواهد نجومی، ممکن است اندازه جهان نامتناهی باشد، و این یعنی جهان تا ابد ادامه دارد. ولی، حتی با استفاده از قویترین تلسکوپهایی که هنوز ساخته نشده‌اند و ممکن است بتوانیم آنها را در آینده بسازیم، ما تنها قادر خواهیم بود قسمت کوچکی از جهان را مشاهده کنیم. در فضا نوعی افق وجود دارد که ما هرگز نمی‌توانیم فراتر از آن را ببینیم، و این افق مشخص کننده حدود چیزی است که به جهان مرئی معروف است. این حدود چیزی نیست که یک مرز واقعی داشته باشد، بلکه ناشی از این حقیقت است که جهان از روز ازل وجود نداشته و اینکه نور مدت زمان معینی طول می‌کشد تا به ما برسد. بعداً، هنگامیکه به توضیح چیزی به نام پارادوکس اولبرس رسیدیم، دوباره به این مطلب بازخواهم گشت.

زمین در مداری که حدود 150 میلیون کیلومتر با خورشید فاصله دارد به دور آن می‌گردد. این فاصله تقریباً معادل است با 4000 برابر طول مدار استوای زمین. خورشید به همراه سیارات خود، تشکیل منظومه شمسی را می‌دهد. یک دور گردش کامل زمین در مدارش 365 روز و 6 ساعت طول می‌کشد، و به همین دلیل است که ما هر چهار سال یک بار، یک سال کبیسه 366 روزه داریم تا جبران آن چهار 6 ساعت اضافی را بکند.

البته اصلاً مناسب نیست تا فواصل عظیم نجومی را با کیلومتر اندازه بگیریم. درعوض اینگونه فواصل بر حسب مسافتی که نور در یک سال طی می‌کند سنجیده می‌شوند. در فصل مربوط به نسبیت خاص خواهیم دید که سرعت نور بالاترین سرعتی است که هر چیزی می‌تواند در جهان دارا باشد [29]. ولی با اینحال مدت زمان معینی طول می‌کشد تا نور از نقطه‌ای مثل A به نقطه‌ای مثل B برسد؛ یعنی این زمان به این بستگی دارد که B چقدر از A دور است. شاید این مورد هنگامی که در اطاق چراغی را روشن می‌کنیم برای ما قابل لمس نباشد. از نظر ما، تمامی اطاق فوراً غرق در نور می‌شود، ولی این تنها به این دلیل است که زمان رسیدن نور از چراغ به اطراف اطاق بسیار کم است. درواقع، این زمان فقط یک میلیاردیم ثانیه است.

ولی در فواصل نجومی، مدت زمانی که نور برای رسیدن از یک مکان به مکان دیگر می‌پیماید کاملاً قابل لمس است. برای نمونه، نور خورشید هشت دقیقه طول می‌کشد تا فاصله 150 میلیون کیلومتری را طی کرده و به ما برسد. درهمین حال این زمان برای اینکه به آخرین سیاره منظومه شمسی، یعنی پلوتو، برسد حدود پنج ساعت خواهد بود. در طول یک سال، نور می‌تواند شصت هزار بار فاصله زمین تا خورشید را طی کند. این مسافت فرضی، که نور می‌تواند در طول یک سال طی کند به سال‌نوری معروف است. (خوب چه نام بهتری می‌توان روی آن گذاشت؟) گرچه تاحدی گیج کننده بنظر می‌رسد که ما از عبارتی استفاده کنیم که معرف یک گستره زمانی است (سال)، درحالیکه می‌خواهیم با آن یک فاصله را اندازه بگیریم، ولی این یک قرار داد است و شما باید این مسئله را در نظر داشته باشید.

اینچنین فواصل عظیم کیهانی مستلزم این است که کیهان‌شناسی فریبندگی‌های خاص خودش را دارد. مثلاً، هنگامیکه با تلسکوپ به ستاره‌ای که یک سال‌نوری با ما فاصله دارد نگاه می‌کنیم، باید بخاطر داشته باشیم آنچه که اکنون می‌بینیم نوری است که یک سال قبل ستاره را ترک کرده و اکنون به ما رسیده است. بنابراین ما ستاره را بصورت آنچه اکنون هست نمی‌بینیم، بلکه حالتی را می‌بینیم که یک سال جوانتر است. در واقع، ما درحال نگاه کردن به گذشته هستیم. در زمین‌شناسی و باستان‌شناسی، دانشمندان در اطراف خود به علائمی (سنگ‌ها، و بقایای فسیلی) نگاه می‌کنند، و سعی دارند حالت گذشته آنها را از آنچه که امروز هستند استنتاج کنند. ولی ستاره‌شناسان می‌توانند مستقیماً به گذشته نگاه کنند. هر چه به دورتر نگاه کنند، تلسکوپ‌های آنها نور قدیمی‌تری را دریافت می‌کند که به گذشته دورتری تعلق دارد. دورترین اجرامی که می‌توان آنها را از زمین مشاهده کرد میلیاردها سال نوری با ما فاصله دارند، و این اجرام تصویری از چگونگی جهان در هنگامی که هنوز خیلی جوان بوده به ما ارائه می‌کنند.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 4

سیاه‌چاله‌ها

$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image001.jpg$

سیاه‌چاله‌ها سوراخ مَقعَد فضا هستند.

بی‌ویس و بات‌هد [30]

نور عجیب‌تر از آنیست که دیده می‌شود!

نور واقعاً چیز عجیبی است. شما احتمالاً وقت زیادی را بر سر این موضوع که نور از چه ساخته شده تلف نکرده‌اید، مگر اینکه قبلاً در زمینه‌های علمی کار کرده‌ باشید. ممکن است فکر کنید که نور مسلماً چیزیست که از اشیائی مانند خورشید، لامپ‌های الکتریکی، مشعل‌ها، شمع‌ها و غیره تابیده می‌شود، و از هر چیزی هم که ساخته شده باشد، به چشمان ما وارد شده و موجب می‌شود تا ما چیزهای مختلف را «ببینیم». هنگامیکه نور از جسمی منعکس و به شبکیه چشم ما وارد می‌شود، اطلاعاتی از شکل و رنگ آن جسم با خود حمل می‌کند. ولی واقعاً خود نور از چه چیزی ساخته شده؟

قبلاً برای شما شرح دادم که وقتی جسمی از ما دور می‌شود چگونه رنگ نور آن، بدلیل کشیده‌تر شدن طول موجش، سرخ‌تر می‌شود. این مسئله بر این دلالت دارد که نور از آن نوع مواد فیزیکی نیست که ما بتوانیم آنها را لمس کنیم. درحقیقت، در مدرسه به ما آموخته‌اند که نور، درست مانند امواج صوتی و یا برآمدگی‌های روی سطح آب، در هنگامی که سنگی به داخل آن پرت می‌شود، فقط نوسانی از امواجِ متناوبِ انرژی‌دار است. تمام آن آزمایشاتی را که احتمالاً در دوران دبیرستان در آزمایشگاه انجام داده‌اید این مورد را تائید می‌کند. چیزهایی نظیر: آزمایش با آینه و امواج نوری که از روی آن منعکس می‌شود، سپس در درون عدسی‌ها متمرکز شده و هنگامی‌که از یک منشور عبور می‌کند، به رنگهایی شبیه به رنگین کمان (که طیف مریی نور نام دارند) شکسته می‌شود.

بعضی از آزمایشاتی که با نور انجام می‌شود می‌تواند مایع تفریح نیز باشد، و بخاطر دارم هنگامی‌که بچه بودم سعی می‌کردم تا جعبه‌های عکاسی درست کنم و می‌خواستم بفهمم این پرتوهای نور که وارد سوراخ کوچکی که در جلو جعبه قرار داشت می‌شدند، چگونه می‌توانند یک تصویر (وارونه) در پشت جعبه تولید کنند. متاسفانه معلوم شده است که نور به آن صورتیکه در مدرسه یاد می‌گیریم چیز ساده‌ای نیست. درحقیقت، نور چنان پدیده مرموزیست که تمام معلمان فیزیک یک پیمان نانوشته را امضاء کرده‌اند و در آن قسم خورده‌اند هرگز ماهیت حقیقی آن را برای بچه‌های ساده و بیگناه افشاء نکنند. هنگامی که بچه‌ها بزرگ می‌شوند، یا بکلی علاقه خود را نسبت به ماهیت نور از دست می‌دهند، و یا خیلی ساده از باور کردن این مطلب سربازخواهند زد که چیزی همچون نور، که در زندگی ما اینقدر مانوس است، بتواند چنان رموزی را در خود داشته باشد و هنوز هم یکی از ارکان عملکرد جهان بحساب آید.

خیلی خوب، شوخی کردم! من تصدیق می‌کنم آن پیمان‌های مخفی که بوسیله معلمان امضاء شده‌اند چیزی شبیه به داستان‌های روالد دال [31] می‌باشند. واضح است که چنین توطئه سراسری برای مخفی نگاه داشتن ماهیت واقعی نور درکار نیست، ولی وقتی گفتم نور عجیب‌تر از آن است که دیده می‌شود، این را خیلی جدی گفتم.

صوت نمونه ساده‌ای از موج است. گفته می‌شود یک جسم وقتی صدا می‌دهد که ملکول‌های هوای اطراف خود را به ارتعاش در آورد. این ملکول‌ها با آنهایی که در اطرافشان قرار دارند برخورد کرده و آنها را بجنبش در می‌آورند، و این کار تا هنگامی که ارتعاش بگوش ما برسند ادامه پیدا می‌کند. پس از آن ملکول‌های هوا که در داخل گوش قرار دارند موجب ارتعاش پرده می‌شوند و مغز ما این پدیده را بعنوان صدا درک می‌کند. ولی ما هیچ وقت نمی‌توانیم بگوییم که ماده‌‌ای، یا چیزی، از این جسم بیرون آمده و به درون گوش ما رفته، و آن بوده که موجب تولید صدا شده است.

در مورد نور اوضاع خیلی فرق می‌کند. در فصل 6 نشان خواهم داد که چگونه نور یکی از ارکان اصلی سرشت فضا و زمان است. فیزیکدان مشهور دیوید بواِم [32] این مسئله را در عبارت زیر خلاصه میکند: «هنگامی که نور را مطالعه می‌کنیم، به عملکردی اساسی خواهیم رسید که بنیادهای هستی در آن ریشه دارد». بمنظور بحث در مورد سیاه‌چاله‌ها، فعلاً بیائید ببینیم که نور واقعاً از چه تشکیل شده است.

ِایزِک نیوتون بر پایه آزمایشات معروفی که با منشورها انجام داده بود، به‌طور راسخی اعتقاد داشت که نور از جریان ذرات ریزی که آنها را کورپُسِل [33] می‌نامید تشکیل شده است. او ادعا می‌کرد که این مسئله واضح است، چون یقیناً نور مانند امواج صوتی رفتار نمی‌کند. پرتوهای نور همیشه در خط مستقیم حرکت می‌کردند (هنوز خیلی مانده بود تا خمیدگی نور توسط گرانش کشف شود) و سایه‌های تندی را تشکیل می‌داد. امواج صوتی می‌توانستند راه خود را درمیان موانع پیدا کنند و بسادگی در گوشه‌های گرد شکسته ‌شوند. امواج صوتی برای عبور خود به یک رسانه نیاز داشتند؛ یعنی یک جسم مادی متشکل از اتم‌ها که وقتی به ارتعاش درمی‌آید، با خود انرژی و فرکانس صوت را حمل کند. به همین خاطر است که در پوسترهای تبلیغاتی فیلم بیگانه [34]‌ این تیتر به چشم می‌خورد «در فضا هیچ کس صدای جیغ شما را نمی‌شنود» و این مسئله کاملاً درست است، چون در فضا هوایی وجود ندارد تا با خود امواج صوتی را حمل کند. ولی نور به هیچ وجه شبیه این نیست و به آسانی در خلاء و فضای خالی منتشر می‌شود.

به همین دلایل نیوتون قانع شد که نظریه ذره‌ای نور صحیح است. ولی همه در این مورد قانع نشده بودند، و بیش از یک قرن طول کشید تا مشخص شود که نظریه نیوتون شامل تمام ماجرا نبوده. در آغاز قرن نوزدهم توماس یانگ کشف کرد دلیل اینکه بنظر نمی‌رسد نور در گوشه‌ها شکسته می‌شود این ‌است که تاثیر آن بسیار کوچک است. طول موج نور در مقایسه با صوت چنان کوچک است که مقدار این شکست را (که پراش نور [35] نام دارد) بسختی می‌توان مشاهده کرد. با اینحال یانگ توانست این شکست را با فرستادن نور از میان دو شکاف بسیار باریک مشاهده کند. او نشان داد وقتی نور وارد شده از سوراخ به صفحه‌ای که در طرف دیگر قرار دارد می‌رسد، ردیفی از نوارهای تاریک و روشن ایجاد می‌کند، بصورتیکه اگر نور از ذرات تشکیل شده باشند، آنگاه توضیح این پدیده با آن غیر ممکن است. این نوارها، که امروز به نام نوارهای تداخلی شناخته می‌شوند، در هر کتاب درسی فیزیک به اینصورت توجیه می‌شوند که در حقیقت آنها برآمدگی‌ها و فرورفتگی‌های امواج بیرون آمده از دو شکاف هستند که یکدیگر را درجاهایی تقویت و در جاهایی خنثی می‌کنند. ما این پدیده را به صورتهای گوناگون در جاهای دیگر نیز مشاهده می‌کنیم، مثلاً در پرتاب دو سنگ به داخل آب و تداخل امواج تشکیل شده با یکدیگر.

بنابراین آیا نیوتون اشتباه می‌کرد؟ آیا در هر صورت نور بیشتر یک پدیده موجی است تا ذره‌ای؟ در پایان قرن نوزدهم فیزیکدان اسکاتلندی جیمز کلرک ماکسول [36] یک سری معادله‌های ریاضی ابداع کرد که نشان میداد آنچه ما به نام نور از آن یاد می‌کنیم در حقیقت جزء طیف وسیعی از امواج هستند که به آنها امواج الکترومغناطیسی گفته می‌شود، و شامل نور مریی، اشعه ایکس، امواج مایکروویو، تابش‌های فرابنفش و مادون قرمز می‌شوند. در این هنگام هیچ ‌گونه شکی در مورد نظریه موجی یانگ باقی نماند. معلوم شده که نور ترکیبی از میدان‌های الکتریکی و مغناطیسی عمود برهم‌اند که درحال ارتعاش هستند و می‌توانند در خلاء منتشر شود. بنابراین رویهم رفته نور یک پدیده موجی بود. آیا این آخر داستان بود؟

نه‌ خیر! خیلی با آخر فاصله داشت. دراینجا آلبرت اینشتین، که برای ارائه یک رساله در سال 1905 برنده جایزه نوبل شده بود (و این هیچ ارتباطی با نظریات نسبیت او نداشت)، وارد ماجرا می‌شود. رساله اینشتین چیزی را شرح می‌داد که به نام پدیده فتوالکتریک معروف است و نشان می‌داد که نیوتون ‌هم، آنقدرها که تصور می‌رفت، در اشتباه نبود و نور در بنیادی‌ترین شکل خود از ذراتی به نام فوتون تشکیل شده است.

خوب پس تکلیف نوارهای تداخلی یانگ چه می‌شود؟ و همینطور امواج الکترومغناطیسی ماکسول؟ معلوم هست اینجا چه خبره؟ قطعاً نور باید تکلیف خودش را روشن کند که بالاخره یک پدیده موجی است یا ذره‌ای؟

کتاب‌های زیادی هست که در آنها شرح داده می‌شود موضوع از چه قرار است. معلوم شده که نور حقیقتاً خصلتی دوگانه دارد. بعضی اوقات ما می‌بینیم بصورت تناوبی، مانند پدیده‌های موجی، و بعضی اوقات هم مانند جریانی از ذرات رفتار می‌کند. این بستگی دارد که ما چه نوع آزمایشی را با نور انجام می‌دهیم! من قبلاً به شما گفتم که نور پدیده غریبی است و اگر شما از این مسئله خوشتان نمی‌آید، پس باید برای درک بهتر این موضوع ثابت قدم باشید. نظریه‌ای که در آن قواعد رفتاری نور شرح داده می‌شود به QED یا الکترودینامیک کوانتومی معروف است، که فیزیکدان آمریکایی ریچارد فین‌من [37]، با همکاری فیزیکدانان دیگر، در اواخر دهه 1940 آن را بسط دادند. همانطور که از نام آن پیداست، الکترودینامیک کوانتومی خود جزء گروه گسترده‌تری از نظریات فیزیک مدرن است که مکانیک کوانتوم نامیده می‌شوند و نه فقط رفتار نور بلکه تمامی ماده و انرژی را در بنیادی‌ترین سطح خود (از سطح اتم به پائین) توصیف می‌کند.

مکانیک کوانتوم در اواسط دهه 1920 توسط عده‌ای از فیزیکدانان اروپایی، از جمله اینشتین، توسعه داده شد. این نظریه به توصیف پدیده‌های وابسته به اتم می‌پردازد، چیزهایی از قبیل اینکه چگونه یک اتم منفرد می‌تواند همزمان در دو مکان مختلف باشد، و یا اینکه چطور سروکله ذرات می‌تواند خود به ‌خود ازجایی پیدا شود و بناگاه سریعاً دوباره ناپدید شود. اگرچه مکانیک کوانتوم تنها نظریه موفق و مهمترین کشف قرن بیستم بوده، ولی برجسته‌ترین فیزیکدانان جهان براین باورند که اگر کسی درمورد نتیجه‌گیری‌های این نظریه درباره جهانی که ما در آن زندگی می‌کنیم ناراحت نمی‌شود، به احتمال زیاد آن را به درستی درک نکرده است. مکانیک کوانتوم شالوده تمامی شیمی مدرن و همچنین الکترونیک می‌باشد. بدون استفاده از این نظریه ما قادر نیستیم تا ساختار بلورها را درک کنیم، دستگاه‌های لیزری بسازیم و یا تراشه‌های سیلیکونی طراحی کنیم. بدون درک قواعد مکانیک کوانتوم، از تلویزیون، کامپیوتر، ماکروویو، دستگاه‌های پخش سی‌دی و بسیاری دیگر از چیزها، که از موهبت فن‌آوری‌های جدید آنها را داریم، خبری نبود. ما موقتاً بحث خود درباره نور را کنار می‌گذاریم تا نقل قولی از اینشتین را مورد توجه قرار دهیم. او این سخنان را در سال 1951 (یعنی چهار سال قبل از مرگش) گفته بود:

«پس از پنجاه سال تفکر عمیق، در پاسخ به این سئوال که "ماهیت بسته‌های نور (فوتون‌ها) چه هستند؟" به جایی نرسیدم. ولی این‌روزها هر علی، نقی و تقی فکر می‌کند که مفهوم آن را می‌داند، درحالیکه در اشتباه است.»

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 5

زمانه در حال تغییر است

$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image001.jpg$

«زمان وسیله‌ای است که جهان از آن استفاده می‌کند تا همه‌چیز به یکباره باهم اتفاق نیفتد»

جان ا. ویلر

«زمان فقط یک کوفتیه که پشت سرهم میاد و میره.»

گمنام

غریبه‌ای در لندن: «ببخشید ساعت چنده؟»

رهگذر در خیابان: « این یک سئوال فلسفیه! چرا از من می‌پرسی؟»[38]

جرالد جیمز ویت‌رو [39]

زمان چیست؟

بگذارید تا یک نکته را روشن کنم. هر آنچه که شما درباره زمان خوانده یا شنیده باشید، حقیقتاً این موضوعی نیست که کسی آن درک کرده باشد. کتابهای زیادی در مورد سرشت زمان وجود دارد، که بخصوص در سالهای اخیر رشد چشمگیری داشته‌اند، و این باعث می‌شود تا در این کتاب مشکل بتوانم به مسائلی بپردازم که در این زمینه جدید هستند، و یا در جاهای دیگری مورد بحث قرار نگرفته‌اند. ولی قصد من این نیست. من چنین حسی را ندارم که باید در میان انبوهی از کتابهای برجسته که درباره موضوع زمان بحث کرده‌اند، جستجو کنم و آنگاه سعی کنم که از زاویه‌ جدید، یا هوشمندتری، که قبلاً مورد بحث قرار نگرفته چیزی را ارائه دهم و مثلاً بگویم: اینست فرضیه من در مورد زمان. البته‌ بسیاری از آنچه که در مورد زمان نوشته شده یاوه‌گویی محض است. بااینحال، برخلاف اینکه ممکن است شنیدن این موارد در آغاز پوچ جلوه کند، همانطور که از کنار آنها رد می‌شوید، بشرطی که کمی در باره آنها تامل کنید، کم‌کم معنا دار می‌شود.

در آغاز کتاب اشاره کردم که از همان اوان کودکی، مجذوب مفهوم زمان بودم، و هنوز هم چنین است. دراین‌مورد من تنها نیستم. در واقع احتمالاً اکثر مردم همینطورند. حقیقت تاسف ‌انگیز این ‌است که درک امروز من از معنای واقعی زمان، بیش از آنروزی که یک بچه ده ساله بودم نیست. من متوجه هستم که بسیاری از قوانین فیزیک اساساً به طریقی با زمان بستگی دارند، و نیز بسیاری از بحث‌های فلسفی که در مورد زمان مطرح است را شنیده‌ام. چیزهایی از قبیل: روند زمان، جهت زمان، واینکه آیا زمان واقعاً وجود دارد یا تنها نوعی وهم است که در درون ذهن انسان پرداخته می‌شود. ولی اینکه آیا واقعاً دراین باره قانع شده‌ام جای تردید است.

باوجود این یک چیز محقق است و آن این ‌است که نظریات نسبیت اینشتین که در آغاز قرن بیستم مطرح شد بسیاری از تصورات کهنه و معمول را برهم زد. من نسبیتِ زمان را در فصل بعدی مورد بررسی قرار می‌دهم. ولی فعلاً شما را به سمت نظریاتی که در فیزیک و فلسفه درباره سرشتِ زمان مطرح هستند هدایت می‌کنم، نظریاتی که بسیاری از آنها خیلی پیشتر از دوران اینشتین مطرح بوده‌اند.

زمان را چه کسی ابداع کرده؟

دیر زمانیست که انسان از سرشت تناوبی زمان آگاه است. شبها از پس روزها سرمی‌رسند و فصول سال دوباره تکرار می‌شوند. ما همچنین از سرشت خطی زمان آگاه هستیم، و منظور از آن این ‌است که گذر زمان از گذشته به آینده است. رویدادهایی که اکنون در گذشته ما قرار دارند، در همانجا خواهند ماند و امکانی برای بازگشت به آنها وجود ندارد و هردم با گذشت زمان به عقبتر و عقبتر رانده می‌شوند.

در آغاز تاریخ بشر لازم بود تا روز را به واحدهای کوچکتری از زمان تقسیم کنند. بدلیل اینکه زمانی که طول می‌کشید تا خورشید از این سو به آن سوی آسمان حرکت کند مقدار (تقریباً) ثابتی بود، بنابراین تعجب‌آور نیست که اولین دستگاه‌های سنجش زمان، ساعت‌های خورشیدی بودند که درحدود پنج هزار سال قبل در مصر اختراع شدند.

تحول مهمی که در قرن شانزدهم در ساخت ساعت بوجود آمد هنگامی بود که گالیله کشف کرد همیشه مدت زمان ثابتی طول می‌کشد تا پاندولی با طول معین یک دور نوسان خود را کامل کند. ولی تنها در اواسط قرن هفدهم بود که اولین ساعتهای پاندولی ساخته شدند. ساخت این ساعتها باعث شد که سنجش زمان با دقت بیشتری از آنچه که قبلاً بود انجام گیرد، و ساعتها به دقیقه‌ها تقسیم شدند، و دقیقه‌ها به ثانیه‌ها. امروزه کم‌کم، ساعتهای پاندولی و دارای چرخ‌دنده، جای خود را به ساعتهای دقیقتری می‌دهند. یک ساعت دیجیتال حاوی بلور کوچکی از کوارتز است که با گذشت جریان برق از آن، می‌تواند در هر ثانیه هزاران بار به نوسان درآید. این نوسانات بقدری منظم هستند که شما می‌توانید اوقات خود را بر اساس آنها تنظیم کنید. باید ببخشید، ولی اگر کوچکترین واحد زمان ما ساعت باشد، و تمام آن قرار ملاقات‌ها، برنامه‌ریزی‌ها و ضرب‌الاجل‌ها بر اساس این واحد اندازه‌گیری می‌شد، آیا می‌توانید پیش خود تصور کنید که زندگی امروز ما چقدر دشوار می‌شد؟

امروزه دقیقترین دستگاه‌های سنجش زمان، ساعتهای اتمی هستند که قادرند با دقت خارق‌العاده‌یی فاصله‌های زمانی را اندازه بگیرند. عملکرد آنها بر این واقعیت استوار است که اگر به بعضی اتم‌ها انرژی داده شود، آنها نوری را از خود تابش می‌کنند که فرکانس آن بستگی کامل با نوع اتم دارد. معروفترین این ساعتها از نوع سزیم هستند، که زمان استاندارد جهانی براساس آنها تنظیم می‌شود.

اگرچه «ثانیه» واحد استاندارد زمان است، ولی این تنها ابداع خود انسان است. اگر درجای دیگری از جهان موجودات هوشمندی باشند، آنها از واحد خودشان برای سنجش زمان استفاده می‌کنند، و مثلاً، مقدار این واحد می‌تواند مدت زمان گردش سیاره آنها به دور خودش و یا به دورخورشیدشان باشد. تا همین آواخر، «ثانیه» را به اینصورت تعریف می‌کردند: ثانیه برابر است با یک‌شصتمِ یک‌شصتمِ یک‌بیست‌وچهارمِ مدت زمانی که طول می‌کشد زمین یک بار بدور خودش بچرخد (یعنی یک روز)[40].

این طریقی بود که درگذشته یک ثانیه بر آن اساس تعریف می‌شد، ولی حالا دیگر اینطور نیست. امروزه، ما چنان در مورد زمان وسواس داریم که دیگر این تعریف برای ما کفایت نمی‌کند. شما توجه دارید که در اینجا مشکلی وجود دارد. معلوم شده که سرعت گردش زمین درحال آهسته‌ شدن است. البته نه به‌اندازه‌ای که شما متوجه آن شوید، بلکه درحد یک ثانیه در هر چند سال. ولی همین کافیست تا ما به لزوم استفاده از دیگر روش‌های اندازه گیری زمان در دنیای پیشرفته امروز پی ببریم. پس بدلیل اینکه تمام اتم‌های سزیم همیشه نوری را از خود تابش می‌کنند که فرکانس آن 9.192.631.770 دور در ثانیه است، دانشمندان تصمیم گرفتند بیانیه‌ای از خود صادر کنند و اعلام کنند که از این پس ثانیه به اینصورت تعریف می‌شود: «یک ثانیه مدت زمانیست که لازم است تا اتم سزیم 9.192.631.770 بار به ارتعاش درآید». این تعریف به زمان جهانی هماهنگ شده [41] معروف است. بنابراین طول یک روز مطابق با زمان جهانی هماهنگ شده برابر است با 9.192.631.770 × 60 ×60 × 24 ارتعاش یک اتم سزیم. بدلیل دقت فوق‌العاده این ساعتها، و برای جبران کندی چرخش زمین، ما باید هر چند سال یک بار، 1 ثانیه به شمار این ساعتها اضافه کنیم، تا آنچه این ساعتها نشان می‌دهند، و آنچه که تعریف زمان بر اساس چرخش زمین نشان می‌دهد، با یکدیگر متفاوت نباشند.

ولی گذشته از اینکه ما چگونه آن را اندازه می‌گیریم، در باره مفهوم خودِ زمان چه می‌توان گفت؟ تا قبل از اینکه ایزک نیوتون کارهایش را در مورد قوانین حرکت منتشر کند، تصور می‌شد زمان به قلمرو فلسفه تعلق دارد تا به علم. ولی، نیوتون بصورت ریاضی شرح داد که چگونه اشیاء بر اثر نیرویی که بر آنها وارد می‌شود بحرکت درمی‌آیند، و چون تمام حرکات و تغییر و تحولات برای اینکه معنی داشته باشند به مفهوم زمان محتاج بودند، او از زمان تعبیری را بدست داد که امروزه به دیدگاه واقع‌نگر (یا رئالیست) از زمان معروف است. همانگونه که در فصل بعد توضیح خواهم داد، هرچند که ما می‌دانیم این برداشت غلط است، ولی هنوز هم این نگرش، که نوعی برداشت «عقل سلیمی» بشمار می‌رود، با ذهن ما عجین است.

زمان از نظر نیوتون مطلق و بی‌وقفه است. او زمان را بعنوان واسطه‌ای می‌داند که وجود آن کاملاً بر خودش استوار است، و خارج از فضا و مستقل از تمام فرآیندهایی که در فضا روی می‌دهد قرار دارد. در این دیدگاه، گفته می‌شود که زمان با آهنگ ثابتی در جریان است، صرفنظر از احساسی که ما غالباً از گذر زمان در ذهن داریم، گویی یک ساعت فرضی کیهانی وجود دارد که مشخص کننده ثانیه‌ها، ساعات و سالهاست. به گفته نیوتون، زمان مطلق است، موجودیست حقیقی و ریاضی. ما هیچگونه نفوذی بر آهنگ گذر آن نداریم و نمی‌توانیم آن را تندتر یا کندتر کنیم. ما بر این حقیقت نیز واقفیم که چگونه برخی اوقات در مورد گذشت زمان قضاوت نادرستی داریم. تصور کنید که در حالی که در یک قطار نشسته‌اید به خواب می‌روید و سفری که بطور معمول یک ساعت طول می‌کشد، درنظر شما تنها ده دقیقه جلوه می‌کند. هنگامی که به ساعت خود نگاه می‌کنید خواهید دید که یک ساعت تمام گذشته، و این مسئله با نگاه کردن به بیرونِ پنجره و دیدن مناظر اطراف مورد تائید قرار می‌گیرد. البته ساعت شما ممکن است خراب باشد، و یا اینکه دلیل سفر ده دقیقه‌ای شما می‌تواند این باشدکه هنگامیکه در خواب بوده‌اید ترن سرعت خود را چند برابر کرده. ولی احتمال این موارد کم است، زیرا ما می‌دانیم زمان‌سنجِ ذهنی انسان چقدر می‌تواند غیر قابل اتکا باشد. همه ما این احساس را در درون خود داریم که زمانِ نیوتونی حقیقتاً «وجود دارد» و در تمام جهان، با یک آهنگ ثابت، درجریان است.

مذاهب عمده جهان همگی در باره سرشت زمان چیزهای برای گفتن دارند. ادیان توحیدی به یک خدای قادر متعال اعتقاد دارند که آفریننده جهان است و خارج از زمان و مکان ماست. گفته می‌شود او واقف است، زیرا نه فقط بر گذشته آگاه است، بلکه آینده را نیز می‌داند. گفته می‌شود او حی‌ و حاضر است، زیرا در تمام مکانها و زمانها حضور دارد. بنابراین وجود یک خدای لایزال که خارج از جهان ما وجود دارد، هیچ منافاتی با برداشتهای فیزیک مدرن از بوجود آمدن جهان (یعنی زمان و مکان) بصورت یک انفجار بزرگ ندارد.

ولی آنچه که موضوع بحث عمده‌ای میان دانشمندان، فیلسوفان و خداشناسان است، نقشی است که خداوند در اداره جهانِ منظمِ از پیش تعین شده نیوتون بازی می‌کند. برطبق برداشتهای ماده‌گرایانه، (حداقل در اساس) این امکان فراهم است تا ما با استفاده از قوانین حرکت نیوتون بتوانیم موقعیت آتی کلیه ذرات جهان را مشخص کنیم. با فرض براینکه تمام ذرات یک مسیر کاملاً مشخص را طی می‌کنند، و تحت نیرویی قرار دارند که خود آن نیز (اساساً) می‌تواند معلوم باشد، پس این امکان وجود دارد تا موقعیت آتی آنها را در هر زمان تعین کنیم، و درنتیجه اوضاع و احوال جهان را در آینده بدانیم. پس در اینجا آینده مشخص است و حالتی از پیش مقدر شده را دارد.

بنظر می‌رسد این نوع دیدگاه‌های تجربه‌گرایانه از جهان، جایی برای اختیارِ انسان باقی نمی‌گذارد، زیرا خود ما نیز از ذرات تشکیل شده‌ایم و از همان قوانینی که بر دیگر اشیاء حاکم است تبعیت می‌کنیم؛ بنابراین احتمالاً آنچه ما از آن بعنوان اختیار یاد می‌کنیم، چیزی بیش از یک فرآیند از پیش تعیین شده در درون مغزمان نیست، و آن نیز مانند تمام چیزهای دیگر از قوانین نیوتون پیروی می‌کند.

البته در عمل ما حتی قادر نیستیم تا موقعیت آتی چند توپ بیلیارد را در موقعی که ضربه‌ای به آنها وارد و به اطراف پخش می‌شوند حساب کنیم، چه رسد به موقعیت تمام ذرات عالم! ولی برطبق این دیدگاه «جبرگرا»، بشرطی که یک کامپیوتر بسیار قوی در دست باشد که کلیه معادلات را محاسبه کند حداقل از نظر اصولی، باید اینکار امکانپذیر باشد. چنین کامپیوتری باید قادر باشد تا برنامه‌ای را به اجرا درآورد که آنچنان پیچیده است که تعداد متغیرهای مجهول آن از تعداد کل ذرات عالم بیشتر است. دلیل این امر این ‌است که برای مشخص شدن وضعیت هر ذره، ما به (حداقل) شش عدد نیاز داریم: سه عدد برای مشخص کردن مختصات آن در فضای سه-بعدی، و سه عدد دیگر برای مشخص کردن سرعت و جهت ذره.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 6

زمان در نظریه اینشتین

$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image001.jpg$

کلاه دوز گفت «آه! درست است، زمان متوقف نمی‌شود. ولی اگر رفتار تو با آن خوب باشد، تقریباً هر کاری که دلت بخواهد برای تو با ساعت انجام می‌دهد . . . مثلاً می‌توانی تا هر وقت که بخواهی ساعت را روی یک و نیم نگاه داری.»

آلیس در سرزمین عجایب، نوشته لوئیس کارول

چه چیز خاصی درمورد نسبیت خاص وجود دارد؟

از یک نظر، فصل حاضر موتورخانه اصلی این کتاب است. تا اینجا من از شما خواسته‌ام تا فضاهایی با ابعاد بالاتر را پیش خود تصور کنید، و یا انتظار داشتم قبول کنید که گرانش می‌تواند فضا و زمان را درهم بپیچاند، و اینکه توقع داشتم حرف‌های مرا در مورد آنچه که فکر می‌کنیم برای کسی که در درون یک سیاه‌چاله می‌افتد قبول کنید. ولی بمنظور اینکه شما بتوانید منطق استدلاهایی که این نتایج بر اساس آنها بنا شده را آسان‌تر درک کنید، من به‌اندازه‌ای که شایسته باشد آنها را از جنبه عمقی مورد بررسی قرار نداده‌ام، زیرا که چنین کاری فراتر از حوصله این کتاب است. ولی این فصل با بقیه فرق می‌کند. من قادر نیستم از این‌مورد صرف نظر کنم و استدلاهایی را مطرح نکنم که ما را بسمت دیدگاه‌های جدیدی که امروز از فضا و زمان داریم سوق دادند. بیشتر این استدلالات بر اساس نظرات اینشتین بنا شده است. در اینجاست که شما به نبوغ واقعی او پی خواهید برد، و امیدوارم نتایج غیرقابل اجتنابی که او مجبور بود حاصل کند، و هنوز هم شگفت انگیز بشمار می‌رود، موجب شود تا او را تحسین کنید.

اینشتین ده سال قبل از آنکه نظریه نسبیت عام خود را در سال 1915 ارائه دهد، نشان داد که چگونه، براساس یک ضرورت منطقی، فضا و زمان با یکدیگر رابطه دارند. همانطور که خواهیم دید، در همینجاست که ایده درنظر گرفتن زمان بعنوان بُعد چهارم مطرح می‌شود. این نظریه به نسبیت خاص معروف شد، و تنها پس از اینکه به کمک این نظریه ساختار «فضازمان» روشن شد، اینشتین توانست توجه خود را به نظریه جامع‌تری معطوف دارد. نظریه اخیر، نسبیت عام نامیده می‌شود و او در آن نشان می‌دهد که چگونه گرانش می‌تواند بر ساختار فضازمان اثر گذارد و آن را خم کند.

اینشتین نظریه خاص خود را در سال 1905، درحالیکه در سالهای میانی دهه بیستم زندگی خود بود، به جهان عرضه کرد. ولی او همواره از دوران نوجوانی خود، با مفاهیمی که او را به این سمت سوق داده بودند، دست و پنجه نرم می‌کرد. باوجود اینکه چند سال بعد، نظریه نسبیت خاص با نوع جامعتر خود یعنی نسبیت عام جایگزین می‌شود، و درحقیقت همین اثبات تجربی نسبیت عام بود که باعث شد در آن زمان شهرت او جهانگیر شود، ولی امروزه اینشتین بیشتر بخاطر نسبیت خاص خود معروف است. در آن زمان حتی مقاله‌ او در مورد نسبیت خاص آنقدر برجسته نبود تا بعنوان مهمترین اثر او بحساب آید. زمان لازم داشت تا اهمیت این کار آشکار شود. بخاطر داشته باشید که او بدلیل تحقیقاتی که درمورد ذره‌ای بودن نور انجام داده بود توانست مورد توجه کمیته داوران نوبل قرار گیرد و نهایتاً در سال 1921 جایزه نوبل فیزیک را دریافت کند. پس چه‌چیزی درمورد نسبیت خاص هست که آنقدر آن را خاص کرده؟[42]

هواداران نظریه نسبیت خاص در میان توده عوام، اغلب سعی می‌کنند شما را گمراه کنند و برای شما شرح می‌دهند که این نظریه بود که فرمول مشهور

E = mc²

از آن حاصل شد. این مسئله صحیح است، و همین فرمول ساده بود که ما را به سمت استفاده بهتر، یا شاید هم بدتر، از انرژی هسته‌ای هدایت کرد. ولی نسبیت خاص عمیقتر از این فرمول است. این تقریباً شبیه به این است که بگوئیم «تنها دست‌آورد انقلاب صنعتی ماشین بخار بود». در واقعیتِ امر، معنای انقلاب صنعتی از یک اختراع منفرد بسیار فراتر می‌رفت. نه فقط قدرت سیاسی از دست ملاکان و اربابان به کارخانه‌داران و سرمایه‌داران منتقل شد، بلکه با تکامل بیشتر موتورهای درونسوز و الکتریسیته، زندگی مردم عادی نیز بکلی تغییر کرد. به همین طریق نسبیت خاص نیز از فرمول E = mc² خیلی فراتر می‌رود. نسبیت خاص منادی انقلابی عظیم در فیزیک بود، و نشان داد که چرا و چگونه تصورات کهنه‌ای که قبلاً در مورد فضا و زمان وجود داشت باید کنار گذاشته شوند و مجموعه‌ای از مفاهیم نوین و نامانوس جایگزین آنها شود، مفاهیمی که تا به امروز ما نتوانسته‌ایم با آنها خو بگیریم و آنها را جایگزین «تصورات کهنه» خود کنیم. اینشتین نشان داد، آن تصوری که اغلب مردم از فضا و زمان به واسطه «حواس معمولی» خود دارند، اشتباه است. از آن موقع تاکنون هر آزمایشی که برای تائید این نظریه انجام گرفته، هر روز با دقت بیشتری صحت گفته‌های او را تائید می‌کنند. ما در این فصل خواهیم دید که چرا حتی پس از گذشت یکصد سال، هنوز هم برای بسیاری از مردم پذیرفتن نظرات او دشوار است.

نیوتون براستی بعنوان شخصی شناخته می‌شود که توانست با ابداع قوانین حرکت، بنای اصلی مکانیک کلاسیک را پایه گذاری کند. این قوانین توضیح می‌دهند که چگونه یک شیء حرکت می‌کند و چگونه نیروهایی مثل گرانش بر روی آنها اثر کرده و موجب افزایش یا کاهش سرعت و یا تغییر جهت آنها می‌شوند. شاید در این میان آشناترین آنها قانون سوم باشد. احتمالاً شما آن را به اینصورت بخاطر دارید که «هر کنشی واکنشی دارد که با آن مساویست و در خلاف جهت آن قرار دارد». ولی این قانون دوم است که یک قانون اساسی محسوب می‌شود و از اهمیت ویژه‌ای برخوردار است (این مسئله کاملاً اتفاقی است که مهمترین قانون ترمودینامیک نیز قانون دوم آن است). این قانون توضیح می‌دهد که وقتی بر جسمی نیرویی وارد ‌شود چگونه رفتار می‌کند.

تمام اجسام متحرک می‌توانند به دو دسته تقسیم شوند: 1- آنهایی که هیچگونه نیرویی را بر خود حس نمی‌کنند (اجسام لَخت)، و بنابراین یا در جای خود ثابت هستند و یا بحرکت خود در خط مستقیم ادامه می‌دهند و 2- آنهایی که تحت تاثیر نیرویی قرار دارند (اجسام شتابدار)، و درنتیجه یا درحال تغییر سرعت هستند و یا جهت حرکت آنها عوض می‌شود. نمونه‌هایی از اجسام دسته دوم شامل اینها می‌شود: یک شیء در حال سقوط، یک ماشین که در حال شتاب گرفتن و یا ترمز گرفتن است، یک ماشین که در سر یک پیچ گردش می‌کند. حتی توپی که روی یک سطح صاف درحال غلطیدن است نیز به این دسته تعلق دارد، زیرا مقاومت باد و اصطکاک هر دو نیروها‌یی هستند که حرکت توپ را کندتر می‌کنند. قوانین حرکت نیوتون تمام حالت‌های فوق را پوشش می‌دهند، آنهم با دقتی که در بیشتر اوقات برای زندگی روزمره ما کاملاً کافیست.

نظریات نسبیت اینشتین خیلی عمیقتر می‌رود و صرفاً به توصیف قوانین حرکت نمی‌پردازد. دلیل اینکه او به دو نظریه نیاز داشت این بود که او می‌باید مابین دو دسته از حرکات بالا تمایز قائل می‌شد. درغیاب گرانش، اجسامی که آزادانه و با تندی ثابت درحرکتند، با نسبیت خاص توصیف می‌شوند. هنگامیکه سروکله گرانش پیدا شود، ما باید به نسبیت عام روی آوریم.

شما قبلاً دیدید که گرچه قوانین گرانش نیوتون در میدان‌های گرانشی ضعیف، مانند کره زمین، بخوبی جواب می‌دهد، ولی آنها نسبت به نظریه‌ نسبیت عام، که خیلی از آنها دقیقتر است، تنها نوعی حالت تقریبی دارند. به همین ترتیب قوانین حرکت نیوتون نیز در برابر نظریه نسبیت خاص، تنها بطور تقریبی جواب می‌دهند. ولی حالا تفاوت این دو وقتی خود را نشان می‌دهد که اجسام با سرعتهای بسیار زیاد در حرکت باشند. برای خیلی از کارهای عادی، مکانیک نیوتونی برای ما کفایت می‌کند. احتمالاً موشکها سریعترین اجسامی هستند که بیشتر افراد قادر به تصور آن هستند، ولی حتی سازمان فضانوردی آمریکا (ناسا) نیز، برای محاسبات مسیر موشکهای خود که بطرف ماه حرکت می‌کنند، از قوانین مکانیک نیوتونی استفاده می‌کند. واضح است آن چیزی که من بعنوان سرعت بالا از آن یاد می‌کنم، و در آن مکانیک نیوتونی درهم می‌شکند و قادر به پاسخ گویی نیست، چیزیست بسیار بالاتر از آنچه موشکهای امروزی توان رسیدن به آن را دارند. در حقیقت نسبیت تنها در مواردی بکار می‌آید که در آن اجسام بتوانند با سرعتهایی نزدیک به سرعت نور حرکت کنند (که مقدار آن سیصد هزار کیلومتر در یک ثانیه است). در بحثهای آتی من مثالهایی را مورد بررسی قرار خواهم داد که اشیاء با سرعتی نزدیک به نور حرکت می‌کنند. این مثالها را فقط بمنظور بهتر مشخص کردن تاثیر نسبیت می‌آورم و شما نباید خیلی آنها را واقعی تصور کنید.

بطور سنتی راه‌های مختلفی هست که نسبیت خاص توسط آنها شرح داده می‌شود. روش معمول استفاده از یک سری معادلات جبری است که تبدیلات لورنتس [43] نامیده می‌شوند. نگران نباشید ما دراینجا این راه را دنبال نخواهیم کرد. روش دوم استفاده از نمودارهای مخصوصی است که نمودارهای فضازمان نامیده می‌شوند. بسیاری از نویسندگان کتابهای غیر فنی برای توصیف نسبیت از این نمودارها استفاده می‌کنند، زیرا احساس می‌کنند تفسیر و درک آنها از معادلات صرفاً جبری آسانتر است. تا حدودی این مورد صحیح است، زیرا بیشتر مردم به دیدن نمودارهای مختلف عادت دارند. در روزنامه‌ها و تلویزیون نمودارهای مختلفی برای توصیف شانس پیروزی احزاب سیاسی در نظر سنجی‌ها و همچنین میزان شاخصهای تورمی بازار بورس دیده می‌شود. بیشتر شرکتها گزارشهای سالانه خود را بصورت نمودارهای میله‌ای، مُدور یا ستونی عرضه می‌کنند. اینچنین روشهای تصویری ممکن است آموزنده‌تر، و تفسیر آنها نیز ساده‌تر باشد. ولی نمودارهای فضازمان مسئله دیگریست. اگر شما اهل ریاضیات باشید، به احتمال زیاد آنها را بسیار مفید خواهید یافت. و اگر هم که اهل ریاضیات نباشید، آنها تقریباً به اندازه معادلات جبری غیرقابل درک خواهند بود. بنابراین من برای توصیف ایده‌های اینشتین از یک روش سوم استفاده می‌کنم: در این روش من تنها از کلمات استفاده خواهم کرد.

شما پیش خود تصور می‌کنید که چرا من بجای این همه مقدمه‌چینی بسراغ اصل مطلب نمی‌روم و آن را شرح نمی‌دهم. اینهمه هیاهو بخاطر چیست؟ ولی نسبیت خاص سزاوار احترام است. نتایج حاصله از آن مایه اصلی بسیاری از کتابهای علمی تخیلی بوده‌اند، و مترادف نام اینشتین قرار گرفته‌اند. بعنوان نمونه من دو پرسش مهمی که امروزه در تمامی فیزیک مدرن مطرح است، و اغلب پرسیده می‌شود، را برای شما نقل قول می‌کنم. هر دو اینها نتایج مستقیم نسبیت خاص هستند. این پرسش‌ها عبارتند از:

· چرا هیچ چیز نمی‌تواند از نور سریعتر حرکت کند؟

· چرا هنگامی که ساعت‌ها با سرعت بسیار زیادی در حرکت باشند کندتر می‌شوند؟ (این کند شدن هیچ ارتباطی با پرت کردن ساعتهای ‌شماته‌دار در صبح‌ زود و خراب شدن آنها ندارد.)

وقتی این پرسشها از من پرسیده می‌شود، جواب معمول من این ‌است که اگر سئوال‌کننده حقیقتاً مایل است تا به اصل ماجرا پی‌ببرد، باید در یک کلاس نسبیت خاص شرکت کند. برای اینمنظور لازم است تا شما چند مرحله را طی کنید تا به این هدف نائل شوید. در این فصل من شما را بسمت این مراحل راهنمائی میکنم. اگر برای شما پاسخ سئوالات مطرح شده مهم نیست و راضی به قبول آنها هستید، پس می‌توانید از خواندن چند صفحه بعدی کتاب صرف نظر کنید، زیرا مسلم است که هیچ چیزی نمی‌تواند از نور سریعتر حرکت کند و حقیقتاً مشاهده شده که ساعتها درهنگامی که با سرعت بسیار بالا حرکت می‌کنند کُند شده‌اند. ولی چون تا اینجا با من آمده‌اید، من به پایداری شما برای ادامه راه اطمینان دارم.

دو چهره نور

بیاد دارید که در ابتدای فصل چهارم برای اینکه بتوانم به بحث سیاه‌چاله‌ها وارد شوم از خواص عجیب نور صحبت کردم. در اینجا نیز دوباره به موضوع نور بازمی‌گردم، البته نه بدلیل اینکه صرفاً مبحث «مفیدی» است، بلکه بخاطر اینکه شالوده کل نسبیت خاص بر این موضوع قرار دارد.

تا اواخر قرن نوزدهم، به مدد کشفیات توماس یانگ [44] (دانشمند انگلیسی که ثابت کرد تصور نیوتون در مورد تشکیل نور از ذرات اشتباه بوده) و جیمز کلارک ماکسول (فیزیکدان اسکاتلندی که کشف کرد نور از امواج الکترومغناطیسی تشکیل شده است)، نشان داده شد که بدون تردید نور مانند امواج رفتار می‌کند. امروزه آزمایشات متعددی وجود دارد که بوضوح، و بزیبایی طبیعت موجی نور را آشکار می‌کند. البته درست است که از آن زمان تا کنون مکانیک کوانتوم نشان داده که نور، تحت شرایط خاصی، می‌تواند مانند جریانی از ذرات نیز رفتار کند، ولی در بحثهای آتی، این طبیعت موجی نور است که مورد نیاز ماست.

یک ویژگی مهم امواج این است که آنها به چیزی نیاز دارند تا از طریق آن بتوانند حرکت کنند؛ یعنی یک رسانا که بتواند ارتعاشات را پخش کند. هنگامی که شما با کسی که پهلوی شما ایستاده مشغول صحبت هستید، امواج صوتی که از دهان شما بیرون آمده و بطرف گوش او حرکت می‌کنند، نیاز به هوایی دارند تا بتوانند از میان آن عبور کند. بطور مشابه، امواج آبی که روی سطح دریا حرکت می‌کنند، این خود آب است که آنها را انتقال می‌دهد، و «برآمدگی‌هایی» که هنگام تکان دادن یک طناب در آن بوجود می‌آید، به خود طناب نیاز دارند تا در طول آن از یک سو به سوی دیگر حرکت کنند. بطور وضوح، بدون داشتن یک رسانا که موج را با خود حمل کند، اصلاً موجی در کار نخواهد بود. به همین دلیل، فیزیکدانان قرن نوزدهم که قانع شده بودند نور یک پدیده موجی است، لازم می‌دانستند تا رسانایی هم برای انتقال آن وجود داشته باشد. و بدلیل اینکه هیچکس چنین رسانایی را مشاهده نکرده بود، آنها باید راهی را برای اثبات وجود آن پیدا می‌کردند.

در آن موقع این رسانا به اِتِر شفاف [45] معروف بود (این اِتِر را نباید با آن گازی که جزء مواد آلی است و در بیهوشی از آن استفاده می‌شود اشتباه کنید) و تلاشهای زیادی برای آشکار سازی آن در جریان بود. اگر اتر وجود داشت، می‌بایست ویژگی‌های بخصوصی از خود داشته باشد. قبل از هر چیز، برای اینکه نور ستار‌گان به ما برسد، اتر باید در سراسر فضا پخش شده باشد. این ماده بایستی در همه‌ جا حضور داشته باشد، حتی در فضای خالی مابین اتم‌ها. یکی دیگر ازویژگی‌های مهمی که اتر می‌بایست داشته باشد این بود که به هیچ وجه نباید با اشیاء مادی کُنشی داشته باشد و درنتیجه وقتی آنها حرکت می‌کنند نتواند بهمراه آنها کشیده شود. این‌مورد برای دانشمندان از خیلی وقت پیش، یعنی از سال 1729، تائید شده بود. دلیل آنهم یکی از ویژگی‌های نور بود که انحراف نور نامیده می‌شود.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 7

پارادوکس سفردر زمان

$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image011.jpg$

دیدیم که چگونه در نظریه نسبیت یک فاصله زمانی بستگی به دیدگاه شما دارد. برای شخصی که با سرعتهای بسیار بالا حرکت می‌کند، یا مدتی را در میدانهای گرانشی قوی بسر می‌برد، زمان کمتری سپری می‌شود. من قبلاً توضیح دادم که چگونه این‌مورد راهی را در برابر ما قرار می‌دهد تا بتوانیم به آینده سفر کنیم. البته چنین موردی حقیقتاً نمی‌تواند بعنوان وسیله‌ای برای فریب دادن زمان درنظر گرفته شود. تنها کاری که ما انجام می‌دهیم این ‌است که سریعتر از بقیه به آینده می‌رسیم. من توضیح دادم که چگونه این قبیل سفرهای زمانی برای ذرات زیراتمی یک چیز عادی محسوب می‌شود، زیرا آنها تنها اجسامی هستند که می‌توانند به سرعت نور نزدیک شوند. بنابراین موئون‌هایی که توسط پرتوهای کیهانی تولید می‌شوند، درطول سفر کوتاهشان در اتمسفر زمین (در مدت زمان بسیار اندکی) به آینده سفر می‌کنند.

مشکلی که درمورد اینگونه سفرهای زمانی وجود دارد این ‌است که یک طرفه هستند. ممکن است ما روزی قادر باشیم به آینده سفر کنیم، حتی آینده‌های دور، ولی تنها راهی که می‌توانیم دوباره به زمان خودمان بازگردیم این ‌است که از آنجا به گذشته بازگردیم. ولی سفر به گذشته بکلی با سفر به آینده فرق می‌کند و مشکلتر از آن است. هنگامیکه دانشمندان از سفر در زمان سخن می‌گویند، بیشتر تمایل دارند تا به گذشته سفر کنند. درطول این فصل هرجا سخنی از سفر در زمان پیش آمد، منظور سفر به گذشته است.

دو راه وجود دارد که می‌توان به گذشته بازگشت. یک راه این است که بطور وارونه در زمان حرکت کرد و به گذشته رسید، که دراینصورت با انتخاب چنین راهی عقربه‌های ساعت شما وارونه حرکت خواهند کرد، و البته (اگر چنین کاری ممکن باشد) شما متوجه تغییر بخصوصی نخواهید شد. چنین سفرهایی به سرعتهایی نیاز دارد که سریعتر از سرعت نور هستند، که برای ما غیر قابل دسترسی می‌باشند و من نیز قصد ندارم دراینجا به آنها بپردازم. روش دیگر این ‌است که بطور مستقیم در زمان حرکت کنیم (در اینجا ساعت شما در همان جهت معمول حرکت می‌کند)، ولی این بار از یک راه پیچ‌خورده در فضازمان حرکت می‌کنیم که شما را به گذشته‌ بازخواهد گرداند (شبیه تاب خوردن در قطارهای تفریحی پرسرعت). اینچنین پیچ‌خوردگی‌هایی در فیزیک به‌نام «خَم‌های بستهِ زمان‌گونه»[46] معروف هستند و در طول دهه 1990 موضوع تحقیقات نظری هیجان‌آوری بوده‌اند. چیزی که ممکن است برای شما تعجب‌آور باشد این ‌است که این‌مورد از حدود پنجاه سال قبل شناخته شده بود و معادلات نسبیت عام اینشتین چنین خم‌هایی را مجاز می‌دانست. ریاضیدان آمریکایی و اطریشی تبار، کورت گودل [47]، در سال 1949 نشان داد که از لحاظ نظری چنین سفرهایی به زمان گذشته امکان پذیر است.

پس اینهمه هیاهو برای چیست؟ سفر به آینده آسان است و سفر به گذشته، اگرچه دشوارتر است، ولی هنوز بکلی از لحاظ نظری رد نشده. پس منتظر چه هستیم؟ چرا هنوز یک ماشین زمان ‌ساخته نشده؟ دلیل مسئله این ‌است که نه‌فقط بوجود آوردن یک خمِ بستهِ زمان‌گونه در فضازمان فوق‌العاده مشکل است، بلکه ما حتی مطمئن نیستیم که چنین کاری از لحاظ نظری امکان دارد یا نه. اینطور که مشخص است، نسبیت عام به ما می‌گوید که ما نمی‌توانیم بکلی امکان سفر در زمان را نفی کنیم، ولی بسیاری از فیزیکدانان امیدوارند با فهم بهتری که در آینده از ریاضیات حاصل خواهد شد، ما به این نتیجه برسیم که چنین چیزی بکلی ممنوع است. و دلیل اینکه چرا فیزیکدانان از این بابت احساس خوبی ندارند این ‌است که سفر در زمان منجر به پارادوکس‌های عجیبی می‌شود. در این فصل من به برخی از این پارادوکس‌ها اشاره خواهم کرد و خواهیم دید که آیا راه گریزی برای اجتناب از آنها هست یا نه.

بعنوان یک دانشمند، برای من صرفِ نشستن و تماشا کردن فیلم‌های علمی‌تخیلی که با موضوع سفر در زمان سروکار دارند همیشه مشکل بوده. بجای اینکه به موضوع فیلم با دیده تردید نگاه کنم (که اکثرا دانشمندان چنین دیدی دارند) و تنها از داستان (معمولاً) بی‌مزه فیلم لذت ببرم، من بیشتر تمایل دارم تا نقایص منطقی داستان را مشخص کنم. مثلاً می‌گویم: صبر کن ببینم؛ اگه این یارو به زمان گذشته رفته و این‌کار و اون‌کار را انجام داده پس حتماً در تاریخ فضولی کرده و ... غیره، و شما احتمالاً خوب می‌دانید منظورم چیست.

واقعاً خیلی تاسف آور است. بیشتر اینگونه فیلمها مزخرف هستند و من نیز مانند بسیاری از مردم تنها جلوه‌های تصویری آنها را دوست دارم. اگر شما تابحال فیلم سینمائی پیشتازان فضا 4: بازگشت به خانه[48] را دیده باشید می‌دانید که من چه می‌گویم. در آن فیلم، کاپیتان کِرک و خدمه سفینه فضایی او از قرن بیست‌وسوم به قرن بیستم بازمی‌گردند. این فیلم حاوی بعضی از صحنه‌های خنده‌دار است، مثلاً هنگامیکه اِسکاتی [49] سعی دارد با کامپیوتر ارتباط برقرار کند، به او گفته می‌شود باید از ماوس استفاده کند و او نیز ماوس را برداشته و توی آن حرف می‌زند!

پارادوکس تِرمی‌نِیتور[50]

دراینجا می‌خواهم نسخه‌ای از داستانی را که در یک فیلم معروف مطرح می‌شود و در آن پارادوکس سفر در زمان به نمایش گذاشته می‌شود، مورد بررسی قرار دهم. فیلم مورد نظر تِرمی‌نِیتور (نابود کننده) نام دارد و در آن آرنولد شوارتزنگر [51] نوعی آدم‌ماشینی فناناپزیر است که بوسیله روبات‌هایی که در آینده برجهان فرمانروایی می‌کنند، به زمان گذشته فرستاده می‌شود. جان کانِر نام رهبر شورشی‌ها است که به طرفداری از انسانها بر علیه روباتها می‌جنگد، و آرنولد قرار است مادر جان را قبل از اینکه او را بدنیا آورد بکشد. شما متوجه هستید که اگر جان اصلاً بدنیا نیامده باشد، آنگاه شورشی‌ها به آسانی شکست می‌خورند. بنابراین روباتها می‌توانند با سربه‌نیست کردن مادرش از شر او نیز خلاص شوند.

البته نه فقط آرنولد ناکام می‌ماند، بلکه قهرمان دیگری که برای محافظت از مادر جان دربرابر آرنولد به زمان گذشته فرستاده می‌شود، دلباخته او می‌شود و با باردارکردن او نهایتاً ... جان کانِر بدنیا می‌آید. بنابراین این شخص درحقیقت پدر جان است. ماموریت او این بوده تا به گذشته باز ‌گردد و مطمئن شود که جان بدنیا می‌آید، و به آنجا منتهی می‌شود که خوش دلیل بودن او می‌شود.

سئوال این است که آیا برای آرنولد امکان این بوده تا سیر حوادث را بصورتی تغییر دهد که آینده طور دیگری رقم بخورد؟ اگر او موفق می‌شد مادر جان را بکشد، آن وقت چه می‌شد؟ هرچند اگر شما طرفدار فیلم‌های علمی‌تخیلی نباشید، داستان فیلم ممکن است تا اندازه‌ای احمقانه جلوه کند، با این‌ وجود داستان خالی از تناقض و سازگار است. هیچ پارادوکسی پدید نمی‌آید، زیرا آرنولد ناکام میماند. در واقع فیلم به‌هیچ وجه بد نیست و جلوه‌های ویژه آن بسیار دیدنی هستند (بله، می‌دانم حتی از ترمی‌نیتور 2 هم بهتر هستند).

مایل بودم این داستان را دوباره بازگویی کنم تا یکی از شاخصترین پارادوکسهای سفر در زمان، که به پارادوکس پدربزرگ [52] معروف است، را مورد تائید قرار دهم.

اگر بخواهیم آن را در شکل اولیه خود بازگوکنیم، این پارادوکس هنگامی مطرح می‌شود که شما به گذشته بازگردید و پدربزرگ خود را قبل ازاینکه مادربزرگتان را ملاقات کند بقتل برسانید. بنابراین نه مادر شما و نه خود شما هرگز بدنیا نخواهید آمد. و اگر شما هیچگاه بدنیا نیامده بودید، درنتیجه پدربزرگتان نیز توسط شما کشته نمی‌شد، و شما می‌توانستید متولد شوید، بنابراین او باز توسط شما کشته می‌شد و ... غیره. این نمونه‌ای است از یک پارادوکس. پارادوکس بمعنای بحثی است که تا ابد ادامه پیدا کند و در یک دور متناقض بیفتد.

بیائید تا با هم سناریو فیلم ترمی‌نیتور را بازنویسی کنیم. فرض کنید روبات‌های متخاصمِ آینده تصمیم بگیرند بجای فرستادن آدم‌ماشینی خوش‌هیکل‌شان به زمان گذشته، که قرار است مادر جان را ازمیان بردارد، آنها خود شخص جان کانِر را دستگیر کنند و با هر کلکی که می‌دانند او را متقاعد کنند تا خودش به گذشته باز گردد و مادرش را بقتل برساند.

اگر او موفق شود چه اتفاقی می‌افتد؟ منظورم این ‌است که اگر مادر جان قبل بدنیا آوردن او کشته شود، آنگاه اصلاً جانی وجود نخواهد داشت. آیا او بسادگی پس از کشتن مادرش از صحنه روزگار محو خواهد شد؟ و اگر او محو شود (و هرگز چنین شخصی وجود نداشته) پس چه کسی مادرش را کشته؟ جان نمی‌توانسته این کار را بکند، زیرا او هرگز بدنیا نیامده!

چند راه مختلف وجود دارد تا بتوان از این بن‌بست خارج شد، و همگی آنها در بسیاری از داستانهای علمی‌تخیلی به شکلهای مختلف مورد بررسی قرار گرفته‌اند. من در اینجا سه سناریو را مورد توجه قرار می‌دهم:

1. همانطور که جان کانر مادرش را بقتل می‌رساند، خودش از صحنه روزگار پاک می‌شود. بوضوح چنین سناریویی قابل قبول نیست. مادر او گلوله‌ای در قلبش دارد که باید از تفنگی شلیک شده باشد و باید کسی ماشه را کشیده باشد. شما نمی‌توانید بگوئید که جان قبل از اینکه به مادرش شلیک کند وجود داشته، زیرا حالا او تاریخ را تغییر داده و اصلاً متولد نشده. گذشته بطور متفاوتی نمود پیدا خواهد کرد (گذشته‌ای بدون جان) و دیگر نیازی نخواهد بود تا روبات‌ها کسی را به گذشته بفرستند (مخصوصاً کسی که اصلاً وجود ندارد) تا مادرِ مورد نظر را بکشد. این توضیح ایجاب می‌کند که حالا دو نوع روایت از تاریخ وجود داشته باشد: در یکی از آنها جان بدنیا آمده و در دیگری او بدنیا نیامده، که هردو با هم نمی‌توانند درست باشند (تناقض).

2. جان نمی‌توانسته مادرش را بقتل برساند زیرا خودش در صحنه حضور دارد. بعبارت دیگر، این حقیقت که او وجود دارد به این معنی است که هر تلاشی که او برای کشتن مادرش بخرج داده باید با شکست روبرو شده باشد. قطعاً چنین برداشتی از گزینه قبلی بهتر است، زیرا تنها یک روایت از تاریخ را در برابر ما قرار می‌دهد. ولی همانطور که بعداً خواهیم دید این‌مورد نیز مشکلاتی را دربر خواهد داشت.

3. هنگامی که جان به زمان گذشته باز می‌گردد، به جهان‌های دیگری که موازی با جهان قبلی او بوده‌اند وارد می‌شود؛ در چنین جهان‌هایی او مجاز است تا جریان تاریخ را تغییر دهد. بنابراین گرچه او قادر نیست تا گذشته خودش را تغییر دهد، ولی می‌تواند گذشته را در دنیای دیگری، که تقریباً یکسان با دنیای قبلی اوست، تغییر دهد. پس هنگامیکه او مادرش را در دنیای دیگری بقتل می‌رساند، او هرگز در آن دنیا متولد نمی‌شود، ولی در دنیای قبلی، مادرش به حیات خود ادامه می‌دهد. تا این اواخر اینچنین توجیهاتی تنها مورد پسند نویسندگان علمی‌تخیلی بود. ولی، چه باور کنید یانه، حالا چنین سخنانی بوسیله برخی از فیزیکدانان، که بدلایل مختلفی مایلند جهان‌های موازی وجود داشته باشند، جدی گرفته می‌شود. من بعداً به این موضوع بازخواهم گشت و نشان خواهم داد که تنها راه ممکن برای پرهیز از چنین پارادوکس‌هایی، جهان‌های موازی می‌باشد.

خیلی‌ها می‌گویند از میان گزینه‌های بالا، ساده‌ترین و معقول‌ترین آنها مورد دوم است. بیائید فرض کنیم که هیچ نوع جهان‌موازی وجود ندارد (چون هیچ مدرکی بر وجود آنها نیست و در صورت نداشتن ماشین‌های زمان، هیچ راهی نیز برای بررسی آنها وجود ندارد). اینجا نیز تنها یک روایت از تاریخ وجود دارد. ما نمی‌توانیم به گذشته بازگردیم و مسیر تاریخ را تغییر دهیم زیرا ما از قبل خاطراتی را بیاد داریم. اساساً آنچه در قبل اتفاق افتاده، اتفاق افتاده و تمام شده.

این به این معنی نیست که گفته شود ما نمی‌توانیم به گذشته بازگردیم و در تاریخ مداخله کنیم. این تنها به این معنی است که اگر چنین کاری را انجام دادیم، این ما بوده‌ایم که موجب شده‌ایم تا چیزها آنطور که در تاریخ روایت شده‌اند، باشند. درنتیجه یک مسافر زمان هرگز نمی‌تواند به گذشته بازگردد و از قتل جان اف. کِنِدی [53] جلوگیری کند، ولی خودش می‌تواند عامل قتل او باشد.

این نوع بازگشت در زمان و مشارکت داشتن در گذشته، بخوبی در سری فیلمهای بازگشت به آینده [54] مورد استفاده قرار گرفته است. در آنجا حوادثی معینی هستند که قبلاً اتفاق افتاده‌اند و هیچ گونه توضیحی نیز برای آنها وجود نداشته است. تنها در ادامه داستان ما متوجه می‌شویم که علت چنین حوادثی اشخاصی هستند که از آینده به گذشته سفر کرده‌اند. بنابراین ما صحنه‌های معینی را دوبار می‌بینیم: اول از دیدگاه شخصیتهایی که در زمان خودشان زندگی می‌کنند و بعداً از دید مسافرهای زمان (که معمولاً نمونه‌های سالخورده‌تر همان شخصیتهای قبلی هستند).

به فیلم‌نامه فرضی من برای فیلم ترمی‌نیتور بازگردیم. جان ممکن است سعی کند تا مادرش را بقتل برساند ولی واضح است که چیزی باید اتفاق بیفتد تا او را از اینکار بازدارد. این عدم موفقیت می‌تواند دلایل مختلفی داشته باشد. مثلاً ممکن است درست در هنگام ارتکاب به قتل دچار احساسات شده باشد. ممکن است تفنگ خالی باشد، یا ماشه گیر کند. ممکن است درست به هدف نزده باشد. درواقع اهمیتی ندارد که چرا او ناکام مانده، مسئله مهم این است که او می‌باید ناکام باشد. اساساً برای اینکه او در آنجا باشد، مادرش باید زنده بماند. من از این معما بعنوان «پارادوکس عدم اختیار» یاد می‌کنم، زیرا این مورد حاکی از این ‌است که مسافر زمان اختیارِ عمل ندارد و نمی‌تواند کارهای معینی را انجام دهد که مسیر تاریخ را بصورتی تغییر می‌دهند که اصلاً سفر او به گذشته را غیر ممکن می‌سازد (اصلاً باید مادری وجود داشته باشد تا شخص توسط آن بدنیا بیاید و بعداً به هرجا که خواست «از جمله گذشته» سفر کند).

هنگامی که شما شروع به فکر کردن درباره چنین چیزی کردید، درخواهید یافت که دراینجا یک مشکل اساسی وجود دارد. آیا این به این معنیست که هر بار جان سعی کند تا چنین کاری را انجام دهد همیشه محکوم به شکست خواهد بود؟ ما می‌توانیم تصور کنیم که روبات‌ها دوباره جان را به زمان خودشان بازگردانند، به او یک داروی «مادرت را بکش» که از قبل قویتر است تزریق کنند، او را تحت آموزشهای بسیار شدید تیراندازی قرار دهند و یک تفنگ کاملاً روغن خورده، بدون‌گیر، پُر از گلوله و بسیار دقیق در اختیار او قرار دهند. او هنوزهم با شکست روبرو خواهد بود. نیازی نیست تا قوانین فیزیک شرح دهند که چرا او همیشه ناکام می‌ماند. تنها چیزی که مهم است جلوگیری از بوجود آمدن پارادوکس و تناقض است.

فیزیکدانان نظری یک آزمایش فکری را ابداع کرده‌اند تا بوسیله آن ببینیم که اگر یک نفر به گذشته بازگردد و با خودش ملاقات کند چه اتفاقی خواهد افتاد. ریاضیات چه چیزی را پیش‌بینی می‌کند؟ برای اینکه مُدل به‌اندازه کافی ساده باشد، فیزیکدانان یک نوع ماشین زمانِ بیلیاردی [55] را در نظر گرفتند. فکر اصلی این ‌است که یک توپ بیلیارد به یکی از سوراخ‌های میز وارد می‌شود و از سوراخ مجاور، منتها در زمان گذشته، بیرون می‌آید. بنابراین این توپ می‌تواند قبل ازاینکه به سوراخ وارد شود با خودش برخورد کند. در این مدل اگر ما تنها حالتهایی را مجاز بشماریم که به یک پارادوکس منتهی نمی‌شوند و به «حالتهای نامتناقض» معروفند، درآنصورت می‌توان بسادگی از بوجود آمد پارادوکس‌ها پرهیز کرد. بنابراین یک توپ می‌تواند در زمان به عقب بازگردد، از یکی از سوراخها بیرون بیاید و با گونه قدیمی خودش برخورد کرده و آن را بسمت سوراخی بفرستد تا قادر باشد به زمان گذشته بازگردد. ولی حالتی که در آن توپ از سوراخی بیرون می‌آید و طوری با گونه قدیمش برخورد می‌کند که آن را به جای دیگری، غیر از سوراخی که باید برود، می‌فرستد، از نظر ریاضی مجاز نخواهد بود زیرا به یک پارادوکس منتهی می‌شود. این ایده بسیار مرتب است و به این معنی است که طرفداران سفر در زمان می‌توانند از این نظر خودشان را تسلی بدهند و از نظر ریاضی ثابت کنند که درصورت بخرج دادن احتیاط، می‌توان از بروز پارادوکس جلوگیری کنند. بدلیل اینکه توپهای بیلیارد آزادی انتخاب ندارند، قبلاً از مشکلی که آنها سعی در پنهان سازی آن دارند اجتناب شده است.

بنابراین قاعده کلی این ‌است که گذشته اتفاق افتاده و ما تنها مجاز هستیم یک روایت از آن را داشته باشیم. این امکان برای ما هست که وقتی به گذشته سفر کردیم، هر کاری که خواستیم انجام دهیم، ولی تا وقتی می‌توانیم چنین کارهایی را انجام دهیم که مداخلات ما در تاریخ همیشه به چیزهایی منجر شود که قبل از سفر ما رخ داده‌اند. حتی در داستان اصلی ترمی‌نیتور نیز آرنولد هرگز نمی‌توانست موفق شود، زیرا او از دنیایی آمده بود که جان در آن زنده بود، و بنابراین حتی نباید اینقدر به خودش زحمت می‌داد تا سعی در بدنیا نیامدن او کند. ولی فکر ‌کنم اگر اینطور بود، فیلم آنقدرها لذتبخش نبود.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 8

کرم‌چاله‌ها

$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image011.jpg$

او گفت : «ببینید دوستان، من متخصص نسبیت عام نیستم. ولی آیا ما هرگز یک سیاه‌چاله دیده‌ایم؟ آیا هرگز به درون آن افتاده‌ایم؟ آیا از آن بیرون آمده‌ایم؟ آیا یک ذره تجربه به خروارها نظریه‌پردازی نمی‌ارزد؟»

واگی با خشم جواب داد «می‌دونم، می‌دونم، باید چیز دیگه‌ی باشه. فهم ما از فیزیک نمی‌تونه آنقدرها هم پرت باشه. می‌تونه؟»

او با صدای غم انگیزی در حالیکه رو به اِیدا داشت آخرین سئوالش را مطرح کرد. اِیدا در پاسخ جواب داد «یک سیاه‌چاله طبیعی نمی‌تونه یک تونل باشد؛ اونا در مرکزشون تکینگی‌های غیرقابل عبوری دارند.»

تماس، نوشته کارل سِیگِن [56]

سفر ما از آغاز زمان شروع شد و به کرانه‌های عالم ادامه یافت. میراثی که از آلبرت اینشتین برای ما به یادگار مانده، واقعیتی را توصیف می‌کند که از هر آنچه خوابش را هم می‌دیدیم شگفت‌انگیزتر و مرموزتر است. پیچ‌خوردگی زمان، سیاه‌چاله‌ها، جهان‌های موازی، گذشته و آینده‌ای که همراه با حال، در کنار هم وجود دارند. حالا دیگر هیچیک از این موارد صرفاً به قلمرو تخیلات علمی وابسته نیستند. همچنین هیچیک از آنها نتیجه تخیلات مُشتی دانشمند دیوانه که دراقلیت قرار دارند نمی‌باشند. کلیه این موضوعات عجیب، نتیجه سالها پیشرفت تدریجی است که اکنون برخی از آنها بعنوان حقایق علمی قلمداد می‌شوند. برای نمونه کند شدن زمان بواسطه گرانش، تنها یک نظریه نیست که ممکن باشد فردا بدلیل آمدن نظریه بهتری ناگهان غلط از آب درآید، بلکه با آزمایشهایی که مرتباً در مراکز علمی صورت می‌گیرد ثابت شده که حقیقتاً صحت دارد. نظرات دیگر، گرچه صحت آنها محتمل است، ولی ممکن است تاب مقاوت در برابر مرور زمان، یا بررسی‌های دقیق و مداوم دانشمندان، را نیاورند. در برخی مواقع اگر معلوم شود که پیش‌بینی‌های یک نظریه با نتایج یک آزمایش در تناقض است، آنگاه آن نظریه بکلی غلط از آب درمی‌آید، یا ممکن است با نظریه دیگری جایگزین شود که پدیده‌های بیشتری را توصیف کند و درک عمیق‌تری از طبیعت را به ما بدهد.

علی‌رقم این حقیقت که ما هرگز با یک سیاه‌چاله‌ روبرو نبوده‌ایم، هم‌اکنون بطور معقولی اطمینان داریم که آنها وجود دارند. شواهدی که برای آنها موجود است بقدری قانع‌کننده هستند که ما نمی‌توانیم توضیح دیگری برای آنها پیدا کنیم. نه فقط وجود سیاه‌چاله‌ها نتیجه غیرقابل اجتناب نظریه نسبیت عام می‌باشد، بلکه ما می‌توانیم آثار غیرقابل تردید آنها را نیز در تلسکوپ‌هایمان مشاهده کنیم.

کرم‌چاله‌ها موضوع کاملاً متفاوتی هستند. معادلات نسبیت عام، که کرم‌چاله‌ها را بعنوان موجودات نظری توصیف می‌کند، وجود آنها را مجاز می‌داند. ولی برخلاف سیاه‌چاله‌ها، کرم‌چاله‌ها بدون داشتن هیچگونه شواهد نجومی که وجود آنها در جهان تائید کند، همچنان بعنوان مباحثی نظری باقی مانده‌اند. از این نظر متاسفم که بر سر موضوعی که هنوز مورد بحث قرار نداده‌ام، آب سردی را خالی می‌کنم و از بامزه بودن آن کم می‌کنم. ممکن است اینکار تنها نوعی واکنش دفاعی باشد که من دربرابر اتهاماتی نشان می‌دهم که توسط فیزیکدانان دیگر مطرح می‌شود و مرا به این متهم می‌کنند که بر روی خطی حرکت می‌کنم که مرز بین حقایق علمی و تخیلات علمی است. بنابراین بمنظور اینکه این فصل را به سوی دیدگاه کسانی که محافظه‌کارتر و شکاک‌تر هستند سوق دهم یک بند از کتاب مَت ویزِر [57] به نام « کرم‌چاله‌های لورنتسی: از اینشتین تا هاوکینگ» را برای شما نقل‌قول می‌کنم. کلماتی که در کروشه نوشته شده از خود من است:

«گرچه فیزیکِ کرم‌چاله‌ها حالت نظری دارد، ولی زیربنای اصلی نظریه‌های آن، یعنی نسبیت عام و فیزیک ]کوانتوم[، هر دو آزمایش شده‌اند و عموماً مورد تائید هستند. ]حتی[ اگر ما بعداً به تنگناهایی بیفتیم که با تناقض‌های مصیبت‌بار و ناشناخته محصور شده، امید آن می‌رود که این چنین مصیبت‌هایی جالب و آموزنده باشند.»

بنابراین ممکن است که کرم‌چاله‌ها وجود نداشته باشند، ولی حداقل مطالعه آنها ممکن است به ما کمک کند تا درک بهتری از کارکرد جهان خود داشته باشیم. اوه، تا یادم نرفته بگویم که آنها هیچ ارتباطی با کرم‌‌ها ندارند.

پلی بسوی جهانی دیگر

ایده اصلی کرم‌چاله‌ها به خیلی وقت پیش، و تقریباً به دوران پیدایش خود نسبیت عام باز می‌گردد. از فصل 4 بخاطر دارید که کارل شوارتزشیلد اولین کسی بود که متوجه شد معادلات نسبیت عام اینشتین وجود سیاه‌چاله‌ها را پیش‌بینی می‌کنند. بعبارت دقیقتر، سیاه‌چاله مورد نظر او حاوی یک تکینگی در مرکز خود بود؛ یعنی نقطه‌ای که چگالی آن بینهایت بود و زمان در آنجا به پایان می‌رسید. در تکینگی، کلیه قوانین شناخته‌شده فیزیک درهم می‌شکنند. این موضوع مایه آزار اینشتین بود. او از این سوراخهای موجود در فضازمان اصلاً خوشش نمی‌آمد و برای او کافی نبود که در یک سیاه‌چاله افق رویدادی وجود دارد که از دنیای خارج در برابر چنین اشیائی محافظت می‌کند. برای او، وجود ناپیدای آنها تنها مانند ضرب‌المثل «از دل برود، هرآنچه از دیده رود» نبود.

در سال 1935 اینشتین به همراه همکارش ناتان رُزِن [58] مقاله‌ای را منتشر کرد که آنها در آن سعی کردند ثابت کنند که تکینگی‌های شوارتزشیلد وجود ندارند. آنها از نوعی تکنیک ریاضی استفاده کردند که تبدیل مختصات نامیده می‌شود، و توانستند جواب شوارتزشیلد را بصورتی بازنویسی کنند که حاوی نقطه‌ای (تکینگی) نباشد که در آن فضا و زمان متوقف می‌شود. ولی راه‌حلِ آنها نیز، خودش به همان اندازه قبلی عجیب بود. آنها نشان دادند که تکینگی مبدل به پُلی شده که جهان ما را با ... یک جهان موازی متصل می‌کند! این جهان موازی، از آن انواعی نیست که در فصل قبل درباره آنها توضیح دادم و نتیجه تقسیم جهان‌ها در مکانیک کوانتوم است. این نوع پُلِ ارتباطی بین دو جهان، امروزه به نام پُل اینشتین-رُزِن [59] معروف است. چنین چیزی از نظر اینشتین، تنها حالت نوعی تمرین نظری در هندسه را داشت که در آن دو فضازمان به هم متصل می‌شوند. او اعتقاد نداشت که چنین پُلی حقیقتاً می‌تواند وجود داشته باشد، درست به همان اندازه که به عدم وجود تکینگی‌ها اعتقاد داشت. از نظر او این تنها می‌توانست نوعی نابهنجاری در ریاضیات نسبیت عام باشد.

بنابراین وجود چنین پُل‌هایی که دو جهان مختلف را بهم متصل می‌کنند، حتی در آن زمان هم شناخته شده بودند. ریاضیدانان قرن نوزدهم خیلی به فضاهای خمیده و ابعاد بالاتر علاقه داشتند. درحقیقت درست نیم‌قرن قبل از اینکه اینشتین کارهای خودش در مورد نسبیت را منتشر کند، ریاضیدانی به نام چارلز داجسون [60] برای کودکان کتابی نوشت که موضوع آن هندسه ابعاد بالا و جهان‌های موازی بود. نام مستعار این نویسنده لوئیس کارول بود و در سال 1865 کتاب آلیس در سرزمین عجایب را منتشر کرد. بیشتر ما با ماجرای این کتاب آشنا هستیم و مثلاً آنجایی که آلیس خرگوش سفید را تعقیب می‌کند، در حقیقت به یک پُل اینشتین – رُزن می‌رسد که به جهان دیگری متصل است. تا آنجا که بخاطر دارم در آنجا به این پل، سوراخ خرگوش می‌گفتند، ولی معنای آن با پل اینشتین- رُزِن یکی است. دلیل اینکه چنین وقایع عجیبی می‌توانست در سرزمین عجایب روی دهد این بود که قوانین فیزیک در دنیای آنها طور دیگری بودند. البته داجسون به این مسئله واقف نبود که چه نوع مکانیسمی می‌تواند موجب شود تا دنیای ما بوسیله یک تونل به دنیای دیگری متصل شود. توجه داشته باشید که این کتاب قبل از مطرح شدن نسبیت، مکانیک کوانتوم و کیهان‌شناسی مدرن منتشر شد. داستان صرفاً بر پایه ایده‌های هندسی بنا شده بود که درباره چگونگی خمیدگی فضا و اینکه چطور دو فضا می‌توانند در ابعاد بالاتر از سه (که به آن اَبَرفضا می‌گویند) به یکدیگر متصل شوند. چیزی که اینشتین پنجاه سال بعد نشان داد این بود که چنین خمیدگی‌هایی هنگامی روی می‌دهند که در یکجا به اندازه کافی ماده (و یا انرژی، چود هر دو معادل یکدیگرند) جمع شده باشد و موجب خمیدگی فضای اطرافش شود. نظریه گرانش او (که همان نسبیت عام باشد) پایه‌های فیزیکی لازم برای توصیف چنین‌ تونل‌هایی را فراهم کرد، گرچه احتمال وجود آنها در جهان واقعی اندک است.

با اینحال در آخرین کتاب داجسون، به‌نام سیلوی و بُرونو که درسال 1890 چاپ شد، ما متوجه می‌شویم که او (و احتمالاً دیگر ریاضیدانان هم‌عصرش) درباره نوعی راه‌ میانبر فکر می‌کردند که نقاط مختلف جهان را بهم متصل کند. در آن داستان، سرزمین پریان و سرزمین‌ بیگانه‌گان هزاران مایل با یکدیگر فاصله دارند. ولی بوسیله نوعی «جاده سلطنتی» به یکدیگر متصل هستند، که شما با پیمودن آن می‌توانید فوراً از یکی به دیگری بروید. همچنین در این کتاب او سفر در زمان، تغییر سرعت ساعتها و معکوس شدن زمان را شرح می‌دهد.

اگر اکنون به سالهای دهه 1930 نگاه دقیقتری بیاندازیم، متوجه می‌شویم که چرا جامعه علمی آنروز درمورد پل اینشتین-رُزِن خیلی هیجان زده نشد. زیرا این پُل، بر خلاف سوراخ خرگوش در داستان آلیس در سرزمین عجایب، هرگز نمی‌توانست برای سفر به جهان‌های دیگر استفاده عملی داشته باشد. یک راه برای اینکه ببینیم چگونه پل اینشتین- رزن می‌تواند شکل بگیرد این ‌است که تصور کنیم تکینگی موجود در جهان ما از انتهای خود، به انتهای تکینگی جهان دیگری متصل است. پس اگر ما به درون یک سیاه‌چاله سقوط کنیم، آیا می‌توانیم به دنیای دیگر سفر کنیم؟ سیاه‌چاله‌ها را مثل عالم بعد از مرگ تصور کنید. هیچکس واقعاً نمی‌داند که وقتی ازاین دنیا رفت چه چیزی درانتظار او خواهد بود، و درست به همین ترتیب تا وقتی ما حقیقتاً به درون یک سیاه‌چاله نیفتاده‌ایم نمی‌توانیم مطمئن باشیم که چه اتفاقی برای ما خواهد افتاد. حتی پس از سقوط هم، ما قادر نخواهیم بود به کسانی که در خارج از افق رویداد منتظر ما هستند، خبری از درون آنها بدهیم. بعنوان یک دانشمند، من مایلم تصور کنم که اطلاع ما در مورد سیاه‌چاله‌ها کمی بیش از عالم پس از مرگ است، زیرا حداقل اولی از معادلات ریاضی تبعیت می‌کند!

پس چه چیزی باعث می‌شود تا نتوانیم از یک پل اینشتین-رزن بعنوان وسیله‌ای برای رسیدن به جهان‌های دیگر استفاده کنیم؟ خوب، در شروع باید بگویم در اینجا افق رویدادی وجود دارد، و هنگامی که شما به داخل یک سیاه‌چاله سقوط می‌کنید، نخواهید توانست از افق رویداد آن بیرون بیائید. البته بمنظور اینکه از طرف دیگر آن بیرون بیائید، این سیاه‌چاله باید به یک سفید‌چاله متصل شده باشد. بخاطر دارید که سفیدچاله‌ها نقطه مقابل سیاه‌چاله‌ها هستند و بجای داخل شدن، همیشه ماده از آنها خارج می‌شود. بنابراین سفید‌چاله‌ها نیز باید با چیزی محاصره شده باشند که حالت عکس افق رویداد را دارد، چیزی که به نام ضِد افق [61] معروف است و تنها اجازه عبور یک طرفه به سمت بیرون را می‌دهد و هرگز اجازه دخول ماده به درون خود را نمی‌دهد. متاسفانه ضد افق‌ها خیلی ناپایدارند و در ظرف چند ثانیه پس از تشکیل‌ به افق‌ رویداد معمولی تبدیل می‌شوند. بنابراین با عبور از افق‌رویداد اولین سیاه‌چاله ، شما به افق‌رویداد دوم خواهید رسید که مانع خروج‌تان از انتهای دیگر می‌شود. تصور کنید که یک زندانی در سلولی گرفتار است و تونلی را در زیر تختخواب خود کشف می‌کند. این تونل چند متری به عمق زمین می‌رود و پس از آن به سمت بالا آمده و در سلول مجاور بیرون خواهد آمد، زندانی متوجه خواهد شد که راه گریزی نیست و این مکان جدید نیز، زندان است.

یک مشکل عمده که در مورد پل اینشتین-رزن وجود دارد این ‌است که کُل سیستم ناپایدار است. ارتباط لازم تنها کسری از ثانیه دوام خواهد داشت و پس از آن بسته می‌شود. درحقیقت طول عمر این تونل بقدری کوتاه است که حتی نور نیز فرصت نخواهد داشت از آن عبور کند. بنابراین اگر شما به امید عبور از یک سیاه‌چاله به داخل آن بپرید، همیشه در دام تکینگی آن گرفتار می‌شوید، و اینکه کسی به سیاه‌چاله سقوط کند و بدن او به اندازه‌ای فشرده شود که حجم آن از یک اتم هم کوچکتر شود هرگز چیز مطلوبی نخواهد بود!

تازه همه اینها با این فرض بود که بدن شما تا قبل از اینکه به تکینگی نرسیده‌اید بواسطه نیروهای جزر و مدی تکه پاره نشود. سیاه‌چاله‌ای که شما قصد عبور از آن را دارید باید از نوع فوق‌سنگین باشد، که حداقل به شما فرصت عبور از میان افق‌رویداد بدهد. رویهم رفته پُل اینشتین-رُزن هرگز نمی‌تواند بعنوان وسیله‌ای برای سفر به جهان‌های همسایه در نظر گرفته شود، و درنتیجه پس از گذشت سالها، هنوز هم تنها بعنوان یک موضوع صرفاً نظری باقی مانده است.

آلیس از درون آئینه

در تاریخ کرم‌چاله‌ها نقاط عطف فراوانی به چشم می‌خورد. پس از کارهای اولیه اینشتین در اواسط دهه 1930، چیز بخصوصی روی نداد تا اینکه جان ویلر، یکی از برجسته‌ترین فیزیکدانان قرن بیستم (و کسی که لغت سیاه‌چاله را ابداع کرد)، در سال 1955 مقاله‌ای را دراین‌مورد منتشر کرد. او برای اولین بار نشان داد تونلی که در درون فضازمان قرار دارد، نیازی نیست تا جهان ما را به یک جهان موازی خودش متصل کند، بلکه می‌تواند طوری خم شود که دو ناحیه مختلف جهان خودمان را به یکدیگر متصل کند (مانند دسته یک فنجان). دراین‌حالت تونل می‌تواند از یک فضازمان معمولی بیرون بیاید و با عبور از میان ابعاد بالاتر مسیر متفاوتی را بین دو «دهانه» خودش بوجود آورد. دوسال بعد، در مقاله‌ برجسته‌ای به نام «هندسه‌پویایی»[62]، که بمعنی مطالعه تغییر و تحولات خواص هندسه فضا می‌باشد، او لغت «کرم‌چاله» را به اصطلاحات فیزیک اضافه کرد. البته در آن موقع هنوز کارهای او صرفاً جنبه نظری داشت. هدف او این بود که بفهمد اشکال مختلف فضازمان چگونه می‌توانند باشند، و کلاً کارهای او ربطی به استفاده از کرم‌چاله‌ها برای سفر به نقاط دیگر جهان نداشت. در حقیقت کرم‌چاله‌های مورد نظر ویلر، از نظر اندازه فوق‌العاده کوچک بودند. او مشغول مطالعه ساختار فضازمان در کوچکترین مقیاس ممکن بود، یعنی همان جایی که مکانیک کوانتوم به ما می‌گوید همه چیزها حالتی مبهم و نامعین به خود می‌گیرند. در چنین مقیاسی، حتی فضازمان نیز حالتی شبیه به کَف خواهند داشت و مبهم می‌شوند و اشکال و ساختار آنها می‌تواند به هرصورتی درآید. این مسئله شامل کرم‌چاله‌های بسیار کوچک، که می‌توانند بصورت تصادفی بوجود ‌آیند، نیز می‌شود. من از اینها به عنوان کرم‌چاله‌های کوانتومی اسم می‌برم و کمی جلوتر در همین فصل به آنها خواهم پرداخت.

رخداد مهم بعدی هنگامی روی داد که در سال 1963 ریاضیدان نیوزلندی روی کِر [63] کشف کرد که معادلات اینشتین می‌توانند نوع کاملاً متفاوتی از سیاه‌چاله‌ها را پیش‌بینی کنند: یعنی سیاه‌چاله‌های چرخنده، گرچه او اولین نفری نبود که به این مسئله پی برد. طولی نکشید که معلوم شد راه‌حل کِر می‌تواند برای تمام ستارگان چرخنده‌ای که به سیاه‌چاله مبدل می‌شوند بکار گرفته شود، و بهمین دلیل چون کلیه ستارگان چرخنده با سرعتهای مختلفی به دور محور خود در گردش هستند، سیاه‌چاله‌های کِر حالتی کلی‌تر و واقعی‌تری از سیاه‌چاله‌های غیرچرخنده شوارتزشیلد داشتند. چیزی که جالب است این ‌است که سیاه‌چاله درقیاس با ستاره اولیه‌ای که از آن تشکیل شده بسیار سریعتر می‌چرخد، زیرا از آن خیلی جمع و جورتر است. (بخاطر دارید که در فصل 4 من این نوع سیاه‌چاله‌ها را با ‌پاتیناژ بازان درحال چرخش مقایسه کردم.) چیزی که موجب شد تا نتایج محاسبات کِر اینقدر مورد توجه قرار بگیرد، طبیعت تکینگی‌هایی بود که در مرکز این سیاه‌چاله‌ها قرار داشتند. برخلاف تکینگی‌هایی که در مرکز سیاه‌چاله‌های شوارتزشیلد قرار داشتند، تکینگی‌های کِر نه دارای اندازه صفر بودند و نه شکل نقطه‌ای‌ داشتند، بلکه درعوض حلقه‌ای شکل بودند. دور تا دور این حلقه، جایی است که تمام ماده در آنجا جمع شده، و ضخامت آن تقریباً صفر است و بنابراین چگالی بینهایتی دارد. در میان حلقه، تنها فضای خالی قرار دارد. چنین تکینگی حلقوی، بسته به جرم و سرعت چرخشی که دارد، می‌تواند دهانه‌ای داشته باشد که انسانها، و یا سفینه‌های فضایی آنها، از میان آن عبور کرده و به سفر بروند [64].

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 9

چگونه یک ماشین زمان بسازیم

$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image011.jpg$

چگونه خورشت اژدها درست کنیم: اول از همه یک اژدها پیدا کنید و بعد ...

مَت ویزِر، کرم‌چاله‌های لورنتسی

حال که به این مرحله از کتاب رسیده‌اید، سرانجام در موقعیتی قرار دارید تا درک درستی از فیزیک مورد نیاز برای ساخت یک ماشین زمان داشته باشید. در فصلهای پیشین من دو نظریه نسبیت اینشتین را مورد بحث قرار دادم، هم نظریه نسبیت خاص، که در آن فضا و زمان در یک فضازمان چهار بعدی با یکدیگر متحد می‌شوند، و هم نظریه نسبیت عام که در آن فضازمانِ مذکور در حضور ماده و انرژی خمیده و پیچیده می‌شوند. ما در این فصل به هر دو نظریه نیاز خواهیم داشت. همچنین سرشت زمان را برای شما تشریح کردم و نیز توضیح دادم که درصورتیکه اصرار داشته باشیم به گذشته سفر کنیم باید بر چه نوع مشکلاتی فایق آییم. اکنون زمان عمل فرار رسیده.

من فعلاً تمام اعتراضاتی که در مورد سفر به زمان گذشته وجود دارد (و کاملاً بحق هم هستند) را به کناری می‌گذارم و نوعی دیدگاه عملگرایانه، و بسیار خوش‌بینانه در پیش می‌گیرم، و فرض می‌کنم تا زمانی که سفر به گذشته توسط قوانین شناخته شده فیزیک منع نشده، برای اینکار جای امیدواری هست. من نشان خواهم داد که چگونه امکان دارد تا ما دست بساخت یک ماشین زمانِ بسیار ابتدایی و ساده بزنیم. این را به حساب این نگذارید که من طرفدار سفر به گذشته شده‌ام، بلکه (فعلاً) دیدگاه‌هایی را بررسی می‌کنم که طرفدار این مورد هستند.

حلقه‌های زمانی

اخیراً مقاله‌ای را می‌خواندم که در یکی از مجلات آخر هفته چاپ شده بود و عنوان آن چنین بود: «آیا می‌شود اینشتین اشتباه کرده باشد؟». من پیش خودم گفتم : «اوه نه، باز دوباره یکی پیدا شد تا با مطرح کردن یه مشت نظریات چِرت، نسبیت خاص را رد کنه». از نظر من، اینکه در جایی بخوانم «ثابت شده که نسبیت خاص غلط است» معادل اینست که بخوانم «بتازگی کشف شده که کره زمین مسطح است». بر اساس آنچه ما از جهان می‌دانیم، هر دو این موارد مضحک بنظر می‌رسند. ولی موضوعی که در آن مقاله مورد بحث قرار گرفته بود نسبیت عام بود، و رویهم رفته چیز تهدید آمیزی هم درمورد آن مطرح نشده بود. این تنها عنوان مقاله بود که گمراه کننده بود.

بسیاری از فیزیکدانان، نسبیت عام را بعنوان زیباترین نظریه علمی می‌دانند که تاکنون کشف شده است. زیبایی این نظریه، در سادگی، ظرافت و غنای معادلات ریاضی بکار گرفته شده در آن است. من تصدیق می‌کنم که تنها بخش بسیار کوچکی از انسانها قادر به درک این زیبائی هستند، زیرا این گروه سالها دانش اندوزی کرده‌اند تا آنها را بفهمند و پی به زیبائی آن ببرند. از نظر بسیاری از مردم، این فرمولها چیزی نیستند، جز یک مشت حروف یونانی. ولی از سوی دیگر، من هم هرگز نتوانسته‌ام سبک کوبیسم را زیبا بدانم و یا آن را بعنوان شکلی از هنر درک کنم. در هرحال، نسبیت عام نه تنها خوش‌آیند فیزیکدانان نظری است، بلکه بارها و بارها بوسیله شواهد تجربی مورد تائید قرار گرفته است. ولی تقریباً در کلیه این آزمایشات، چیزهایی که مورد تائید قرار گرفته‌اند در موقعیتهایی بوده‌اند که به آنها «محدوده میدان‌ ضعیف» گفته می‌شود (منظور میدانهای گرانشی ضعیف است). در حالتهایی که نسبیت عام بطور اساسی از گرانش نیوتونی فاصله می‌گیرد (یعنی میدانهای گرانشی قوی)، هنوز هم جا دارد تا سرشت واقعی خود را به اثبات برساند.

مقاله‌ای که در بالا به آن اشاره کردم، آزمایش جدیدی را شرح می‌دهد که یکی دیگر از پیش‌بینی‌های نسبیت عام را، که به امواج گرانشی معروف هستند، مورد تاکید قرار می‌دهد. در حقیقت اولین بند از مقاله حاکی از این بود که درصورتیکه چنین امواج گرانشی یافت نشوند آنگاه نسبیت عام به دردسر خواهد افتاد. ولی اعتقاد فیزیکدانان به این نظریه چنان زیاد است که امیدوارند بزودی نتایج آزمایش‌های جدید معلوم شود و آنچه را که بدنبال آن هستند بزودی پیدا کنند. متاسفانه سرتیتر مقاله‌ای که ادعا می‌کرد : «بزودی اثبات تجربی صحت گفته‌های اینشتین آشکار می‌شود» آنقدرها هم ارزش خبری ندارد، چون از خیلی وقت پیش چنین تجربیات و آزمایشاتی شروع شده‌اند.

امواج گرانشی اختلالات، یا پستی و بلندی‌هایی، هستند که بواسطه حرکت اجسام سنگین در بافت فضا بوجود می‌آید. مانند فصل دوم، بازهم فضا را مانند یک لاستیک ترامپولین تصور کنید. هنگامی که شما در مرکز این ترامپولین ایستاده‌اید، وزن شما باعث خواهد شد تا در درون آن یک فرو رفتگی بوجود آید. این یک راه ساده برای تجسم کردن چگونگی تاثیر جرم بر فضای اطراف آن است. همانگونه که وقتی سنگی را به داخل یک حوضچه پرت می‌کنیم و امواج آب در آن پخش می‌شوند، اگر شما نیز در جای خود شروع به بالا و پائین پریدن کنید، باعث خواهید شد لاستیک به لرزش بیفتد و درصورتیکه لاستیک مساحت خیلی زیادی داشته باشد، این لرزشها نیز در سراسر آن پخش خواهند شد. به همین نحو، سقوط جسم بسیار سنگینی مانند یک ستاره به داخل یک سیاه‌چاله نیز موجب می‌شود امواج مشابه‌ا‌ی، نه در درون فضا، بلکه از خود فضا فرستاده ‌شود که بر کلیه اجسام قرار گرفته بر سر راه این امواج تاثیر خواهد گذاشت. امید می‌رود آزمایشاتی که بر روی زمین انجام می‌شود بتوانند تاثیر این امواج گرانشی را بر روی دستگاه‌های فوق‌العاده حساس آشکار کنند. این دستگاه‌ها بقدری حساسند که اگر چنین امواجی از درون آنها عبور کنند، اندکی منبسط / منقبض می‌شوند.

البته امواج گرانشی هیچ ارتباطی با ماشین‌های زمان ندارند. من تنها بعنوان یکی از پیش‌بینی‌های صریح نسبیت عام، که هنوز هم باید بصورت تجربی مورد تائید قرار بگیرد، ‌به آنها اشاره کردم. ولی نسبیت عام بقدری غنی است که این اجازه را می‌دهد (البته بطور نظری) که اشکال بسیار مرموزتری از فضازمان نیز وجود داشته باشند، که ما آنقدرها به صحت وجود آنها اطمینان نداریم. یکی از این اشکال که به بحث جاری در این فصل مربوط می‌شود چیزیست که خَم بسته زمان‌گونه نام دارد. خَم بسته زمان‌گونه مسیری دایره‌‌ای شکل در میان فضازمان بهم‌پیچیده است که در آن زمان به شکل یک دایره تابیده شده است. اگر قرار باشد شما در چنین مسیری حرکت کنید، بنظر شما اینطور خواهد رسید که انگار در یک فضای معمولی حرکت می‌کنید. درصورتیکه شما درطول این سفر ساعت خود را بازبینی کنید، خواهید دید که بطور معمول بجلو حرکت می‌کند. ولی پس از گذشت مدتی، شما مطابق با ساعتی که در آغاز حرکت در همان‌ مکان بجاگذاشته‌اید، نهایتاً به همان مکان، و همان زمان، اولیه‌ باز خواهید گشت. چنین مسیری ایجاب می‌کند که شما در قسمتی از سفر خود به گذشته سفر کرده باشید. البته درصورتیکه در زمان به عقب بازگشته باشید، این امکان نیز وجود دارد تا به همان مکانی بازگردید که از آنجا حرکت خود را پیش از عزیمت شروع کردید، در غیر اینصورت شما هیچ سودی از سفر خود نخواهید برد. هرگونه انحناء بیشتر در فضازمان موجب می‌شود تا حلقه زمانی شما را به گذشته دورتری ببرد.

«خم بسته زمان‌گونه» اصطلاحی است که معادل همان «ماشین زمان» خودمان است و از این پس از آنها تحت عنوان «حلقه‌های زمانی» یاد خواهم کرد. از خیلی وقت پیش معلوم شده بود که نسبیت عام اجازه وجود چنین حلقه‌های زمانی را می‌دهد، ولی هر زمان سروکله یکی از آنها در معادلات ریاضی ظاهر می‌شد، معمولاً با این استدلال که فرض‌های اولیهِ وارد شده به معادلات غیر معقول بوده‌اند، اهمیت چندانی برای آنها قائل نمی‌شدند. این فیزیکدان‌ها عجب مردمان حال‌گیری هستند! ولی متاسفانه این خلق و خوی آنها کاملاً موجه است و مثالهای متعدد دیگری وجود دارند که نمایانگر این مورد هستند. مثال ساده زیر را درنظر بگیرید: اگر بشما بگویند مساحت یک مربع 9 متر مربع بوده، آنگاه شما بسادگی نتیجه می‌گیرید که طول ضلع آن 3 متر بوده است، زیرا بطور روشن مساحت مربع می‌شود 9=3×3. ولی از طرف دیگر ما می‌دانیم 3- × 3- هم برابر 9 می‌شود (بخاطر دارید که منفی در منفی، می‌شود مثبت). ولی ما هیچ موقع از مربعی که طول ضلعش 3- متر باشد صحبت نمی‌کنیم و بنابراین از (3-) بدلیل غیر واقعی بودن صرف نظر می‌کنیم. معادلات ریاضی که توصیف کننده جهان واقعی هستند، معمولاً به همراه جوابهای صحیح، جوابهای غیر واقعی و بی‌معنی نیز می‌دهند که باید نادیده انگاشته شوند. برای اکثر دانشمندانی که بر روی نسبیت عام کار می‌کنند، حلقه‌های زمانی هم در همین دسته جای می‌گیرند. آنها به این دلیل غیر واقعی تلقی می‌شوند چون سفر به زمان گذشته مشکلات زیادی را دربر دارد.

ولی در سالهای اخیر برخی از فیزیکدانان در رد کردن آنها مردد بوده‌اند و بهمین دلیل مطالعه آنها رواج پیدا کرده است. همانطور که خواهیم دید، بخشی از این فراگیری، مربوط به کارهایی است که کیپ تورن درباره کرم‌چاله‌ها انجام داده است. ولی با وجود اینکه حلقه‌های زمانی را می‌توان بسادگی از حل معادلات اینشتین حاصل کرد، فیزیکدانان هنوز هم مردد هستند که آیا واقعاً چنین چیزهای می‌تواند در جهان ما وجود داشته باشد یا نه.

اولین جواب معادلات میدان نسبیت عام اینشتین، که فضازمانی را توصیف می‌کرد که حاوی حلقه‌های زمانی بودند، در سال 1937 توسط فیزیکدان هلندی ویلِم وَن استوکُم [65] مطرح شد. ولی رابطه بین این جواب عجیب ریاضی و امکان استفاده از آن برای توصیف سفر در زمان، سالها بعد مشخص شد. راه‌حل وَن استوکُم به یک استوانه بسیار بلند نیاز داشت که خیلی چگال باشد و در یک فضای خالی، بسرعت درحال چرخش باشد؛ این‌مورد یکی از آن چیزهای است که شما هیچ موقع آنها را بطور تصادفی در جایی نخواهید دید مگر اینکه سوار بر سفینه فضایی اِنتِرپرایز [66] شده باشید. نسبیت عام پیش‌بینی می‌کند آن نواحی از فضازمان که استوانه را احاطه کرده باشند، به دور آن تاب خواهند خورد و این می‌تواند یک حلقه زمانی را نیز در خود داشته باشد. ولی معلوم بود که طرح استوانه‌های بسیار بلند، خیلی جدی گرفته نشدند و بدلیل اینکه خیلی نامعقول بنظر می‌رسیدند، رد شدند. از آن گذشته، ریاضیات پیش‌بینی می‌کرد که حتی فضازمانی که در فاصله بسیار زیادی از این استوانه قرار دارند، خواص عجیبی خواهند داشت، و این ثابت کننده این‌مورد است که چنین استوانه‌هایی در جهان ما وجود ندارند، والا اگر در آنسوی جهان هم قرار داشتند، ما قادر بودیم تاثیرات آنها را بصورت محلی مشاهده کنیم.

حقیقتاً کارهای کورت گودِل در سال 1949، موجب شدند تا حلقه‌های زمانی به یکی از عنوانهای خبری مهم در محافل علمی مبدل شوند. در مقاله‌ برجسته‌ای که گودل منتشر کرد، او بطور ریاضی نوعی جهان انتزاعی [67] را توصیف کرد که دربردارنده حلقه‌های زمانی بودند. ولی جهان گودل با آن جهانی که ما در آن ساکنیم از یک نظر فرق داشت و آن هم طریقی بود که این جهان پایداری خودش را در برابر فشار رو به درون گرانش حفظ می‌کرد. جهان گودل، بجای اینکه مانند جهان ما انبساط پیدا کند، درحال چرخش بود. درصورتیکه یک مسافر فضایی در چنین جهانی از یک مسیر گِرد که به ‌اندازه کافی طولانی باشد عبور می‌کرد، آنگاه به همان زمان و مکانی می‌رسید که عزیمت خود را از آن شروع کرده. آری، نمونه آشکاری از سفر در زمان!

گرچه اینشتین، که خودش هم مانند گودل در همان ساختمان موسسه مطالعات پیشرفته پرینستون کار می‌کرد، ابتدا از این نوع نتیجه گیری آشفته شده بود، ولی بزودی او (و بسیاری دیگر از فیزیکدانان) بدلیل وابستگی اندکی که این جهان فرضی با جهان واقعی داشت (زیرا ما ما می‌دانیم که جهانمان نمی‌چرخد)، نتایج حاصله را رد کردند. حتی خود گودل هم امکان سفر در زمان را رد می‌کرد، زیرا به انجام رسانی چنین کاری در عمل غیر ممکن بنظر می‌رسید، آنهم نه بدلیل اینکه مدل فرضی او شباهتی به جهان واقعی نداشت، بلکه از این نظر که سرعتهای لازم برای اینکار و نیز مسافتهایی که یک سفینه باید در چنین جهانی بپیماید تا یک حلقه زمانی را کامل کند، بسیار غیر واقعی بنظر می‌رسیدند. ولی این حقیقت به جای خود باقی بود که گودل توانسته بود طرحی را ارائه دهد (ولواینکه غیر واقعی هم باشد) که در آن هیچ یک از قوانین فیزیک نقض نشده‌اند و کاملاً با نسبیت عام هم سازگاری دارد، و تنها مشکل آنها این ‌است که شامل حلقه‌های زمانی است که دربردارنده پارادوکس‌های سفر در زمان هستند. بیشتر فیزیکدانان اعتقاد داشتند، و هنوز هم دارند، که سرانجام از طریق فهم بهتر طبیعت، خلل موجود در قوانین فیزیک، که اجازه اینگونه جواب‌ها را می‌دهند، پر شوند و چنین نتایجی باطل اعلام شود. تا زمانی که چنین چیزی اتفاق بیفتد، جهان گودل بعنوان یکی از شگفتی‌های ریاضی مطرح خواهد بود.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

فصل 10

چه می‌دانیم؟

$Description: Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\black holes\sum_files\image011.jpg$

«اکنون من بر این باورم که حتی اگر بجای سئوال فوق یک سئوال ساده‌تر هم پرسیده بودم- مثلاً اینکه معنی جرم چیست، یا شتاب کدام است، که در دنیای علم معادل "سواد داری یانه؟" هستند- مطمئنم که درمیان هر ده نفر دارای تحصیلات عالیه، تنها یک نفر از آنها متوجه می‌شد که منظور من چیست. بنابراین عمارت رفیع فیزیک مدرن بالا می‌رود، و اکثر باهوشترین افراد مغرب زمین همانقدر از آن آگاهی دارند که نیاکان عصر حجری آنها.»

سی‌.پی اسنو [68]، دو فرهنگ

«دانش امروز ستارگان را تنها مشتی از کُرات متشکل از اتم‌های گازی میداند. شاعران می‌گویند علم با چنین توصیفی که از ستارگان داده، از زیبائی آنها کاسته ‌است. ولی بر هیچ چیز نمی‌توان صفت «تنها» را اطلاق کرد. من هم در شبهای کویر ستارگان را دیده‌ و عظمت آنها را حس کرده‌ام. ولی آیا درست دیده‌ام؟ وسعت کائنات موجب پرواز خیال من هم بوده است- چشمان کوچک من، سردرگم در این گردونِ دوار، تنها قادرند یک میلیون سال نوری را ببینند؛ نقش گسترده‌ای که من هم جزئی از آنم ... ولی آن نقش چیست، معنای آن چیست، یا اصلاً چرا باید باشد؟ اگر کمی بیشتر بدانیم، بازهم چیزی از معمای آن کاسته نمی‌شود. حقیقت جهان هستی از هرآنچه هنرمندان در گذشته تصور می‌گردند شگفت‌انگیزتر است. چرا شاعران معاصر از این شگفتی سخن نمی‌گویند؟»

ریچارد فین‌من [69]، درسهایی از فیزیک، جلد اول

مایلم در این فصل پایانی، از آنچه اعتقاد داریم درباره جهان خود می‌دانیم و فکر می‌کنیم در جهت پیشرفت ما قرار دارد، نوعی ارزیابی به شما ارائه دهم.

نظریه همه چیز، مادر تمام ‌نظریه‌ها

نظریه گرانش هندسی اینشتین (یا همان نسبیت عام) و مکانیک کوانتوم دو دست‌آورد فیزیک قرن بیستم بوده‌اند که بر بالای هرچیز دیگری که ما درباره جهان مادی (و حتی فراتر از آن) ‌دانسته‌ایم قرار گرفته‌اند. از هنگامیکه این دو نظریه توانستند به اتفاق یکدیگر بیشتر وجوهِ اساسیِ واقعیات جهان را تشریح کنند، نظریات دیگر را به حاشیه راندند. همانگونه که در فصل قبلی توضیح دادم، مشکل این است که این دو نظریه با هم سازگار نیستند. هریک از آنها برپایه‌های مختلفی از ریاضیات تکیه زده‌اند و بطورکلی قواعد و اصول جداگانه‌ای دارند. نسبیت عام در تکینگی‌ها و «حلقه‌های‌ زمانی‌ بسته» از کار می‌افتد، حال آنکه مشکل مکانیک کوانتوم این ‌است که قادر نیست تا در چهارچوب اصلی خودش گرانش را توضیح دهد. بنابراین سئوالی که در اینجا مطرح می‌شود این است که ما تا چه حد به داشتن یک گرانش کوانتومی نزدیک شده‌ایم؛ یعنی نظریه‌ای که بتواند همه چیز را توصیف کند، چیزی که به «نظریه همه چیز» معروف است و در ساختار ریاضی خود هم دربردارنده اصول مکانیک کوانتوم است و هم نسبیت عام؟ خوب، همانگونه که قرن بیستم و نیز آغاز قرن بیست و یکم را پشت سر می‌گذاریم، چنین به نظر می‌رسد که ممکن است پایه‌های چنین نظریه‌ای آماده شده باشد.

اینشتین نظریه نسبیت عام خود را در سال 1915 تکمیل کرد، و پس از آن نقش اندکی (آن هم بطور ناخواسته) در توسعه نظریه مکانیک کوانتوم داشت که بتازگی مطرح شده بود و بیشتر فیزیکدانان برجسته آن زمان را بمدت ده سال بخود مشغول کرده بود. ولی هنگامیکه طرحها و اصول ریاضی این نظریه مشخص شد، دیگر چه کاری برای انجام دادن باقی مانده بود؟ با نبوغی که اینشتین داشت، او کسی نبود که با پرداختن به جزئیات بی‌اهمیت راضی شود. درنتیجه سی سال باقی مانده از عمرش را وقف تحقیق در مورد چیزی کرد که به نظریه «میدان وحدت یافته» موسوم است؛ یعنی نظریه‌ای که نسبیت عام را نه با مکانیک کوانتوم، بلکه با نظریه نور (یا بعبارت دقیقتر الکترومغناطیس) ترکیب کند، که البته در این‌مورد زیاد توفیق نداشت. او در این راه روشهای متعددی را آزمود، ولی هرگز موفق به تکمیل آن نشد. گفته می‌شود که پس از مرگش، مقالاتی بصورت ناقص بر روی میز کارش پیدا شدند که در مورد این نظریه بود.

برازنده‌ترین، و در عین حال گیج کننده‌ترین، طرح ریاضی که می‌توانست بعنوان جانشینی برای نظریه وحدت یافته‌ای که اینشتین به دنبال آن بود بحساب آید، نظریه‌ای بود که برای نخستین بار توسط دو ریاضی‌دان مطرح شد: یک لهستانی به نام تئودور کالوزا [70]، و یک سوئدی به نام اسکار کلاین [71]. کالوزا کلیه کارهای اصلی را انجام داد و در سال 1919 نتیجه کارهای خود را بصورت مقاله‌ای برای اینشتین فرستاد. در این مقاله او راهی را پیشنهاد کرده بود که می‌توانست تابش امواج الکترومغناطیسی را در چهارچوب نسبیت عام توضیح دهد.

کالوزا نشان داد تنها کاری که لازم است انجام گیرد این ‌است که معادلات اینشتین بجای اینکه در یک فضازمان چهاربعدی نوشته شوند، با اضافه کردن یک بعد فضایی دیگر، آنها را در یک قالب پنج-بعدی باز نویسی کرد. گرچه چنین چیزی خیلی پرت به نظر می‌رسد و با آنچه ما از حقیقت درنظر داریم بسیار فاصله دارد، ولی از نظر ریاضی انجام دادن آن کار نسبتاً ساده‌ای است. در دنیای ریاضیات ما می‌توانیم هر تعدادی از ابعاد که بخواهیم به فرمول‌ها اضافه کنیم. ولی آیا این بُعد چهارم فضایی که کالوزا آن را مطرح کرد، یک بُعد واقعی بود؟ اگر هم چنین چیزی واقعیت داشته باشد، یقیناً ما از آن اطلاعی نداریم. ولی هنگامیکه کالوزا این بعد اضافی را به فرمولهای خود اضافه کرد متوجه شد که نور، بجای اینکه نوعی میدان الکترومغناطیسی نوسان کننده در میان فضای سه بعدی باشد، درحقیقت نوعی نوسان در این بعد پنجم است. دراینجا باید گفت «حالا بیا و درستش کن». ولی نگران نباشید، خود من هم معنای واقعی آن را درست نفهمیده‌ام! تنها چیزی که می‌توانم در این مورد بگویم این است که چنین رویکردی می‌تواند منشاء نور را در سطح هندسی بنیادی‌تری توصیف کند، درست شبیه همان رویکردی که اینشتین برای توصیف گرانش بعنوان نوعی از انحناء در فضازمان چهار بعدی اتخاذ کرد. باید به این نکته نیز اشاره کنم که نه فقط درنظر گرفتن چنین بعد فضایی مشکل است، بلکه این بعد اضافی مانند سه بعد دیگر فضایی بصورت خطی گسترش پیدا نکرده بلکه بر روی خودش تابیده شده است. یک راه ساده برای نشان دادن چنین چیزی این است که یک فضای دو بعدی را درنظر بگیرید و فرض کنید که این سطح دو بعدی را به دور خودش تابانده‌ایم تا یک استوانه تشکیل شود. یکی از ابعاد این سطح دو بعدی (آنکه ارتفاع استوانه را تشکیل می‌دهد) ثابت مانده، درحالیکه بُعد دیگر آن پیچ خورده و بصورت یک دایره درآمده است.

البته مشکل اصلی این بود که هیچگونه مدرک تجربی که حاکی از وجود چنین بُعد اضافی باشد در دست نبود. گرچه اینشتین تحت تاثیر روشی که کالوزا برای متحد کردن نور و گرانش اتخاذ کرده بود قرار گرفت، ولی حتی خود او نیز تمایل چندانی برای پذیرش این واقعیت که بعد پنجمی وجود دارد نداشت. بهرحال در آغاز کار بر روی نسبیت، حتی قبول ایده یک فضازمان چهار بعدی نیز برای او دشوار بود. ولی حداقل این چهار بعد کنونی (یک بعد زمان و سه بعد فضا) واقعی و قابل درک بودند. عمده‌ترین دلیلی که اینشتین و دیگر دانشمندان شکاک برای رد چنین نظریه‌ای داشتند این بود که ما هرگز قادر به دیدن این بعد فضایی اضافه نخواهیم بود. ولی، پاسخ این سئوال هنگامی مشخص شد که در سال 1926 اسکار کلاین اظهار داشت دلیل اینکه ما نمی‌توانیم چنین بعد اضافی را آشکار سازی کنیم این است که این بُعد چنان بصورت یک دایره بسیار کوچک بر روی خودش جمع شده که قطر آن حتی از یک اتم هم کوچکتر است. بازهم آن سطح دو بعدی را که بر روی خود تاب خورده و تشکیل استوانه‌ای داده پیش خود مجسم کنید. کلاین گفت قطر این استوانه بقدری کوچک است که مانند یک خط به نظر می‌رسد. پس دراین‌حالت آن سطح دو بعدی تاب خورده، همچون یک خط یک بعدی به نظر می‌رسد و ما می‌توانیم بگوئیم که بعد دیگر آن پنهان است. از این نگران هستم که نمی‌توانم برای روشن‌تر شدن این مورد مثالی با ابعاد بالاتر برای شما بیاورم، زیرا همانگونه که در فصل اول نیز توضیح دادم، ما برای خم کردن یکی از ابعاد سطح دو بعدی نیاز به یک فضای سه بعدی داریم. و معلوم است که خم کردن یکی از ابعاد فضاهای بالاتر گیج کننده‌تر می‌باشد.

ولی بقول معروف «هنوز هم کجاش را دیدی!» به خواندن ادامه دهید تا معلوم شود موضوع از این هم پیچیده‌تر است.

پس از گذشت دهه‌ها که نظریه کالوزا-کلاین به فراموشی سپرده شده بود، سرانجام دوباره در اواخر دهه 1970 به صحنه باز گشت. ولی در این موقع نظریه وحدت‌یافته‌ای که بیشتر فیزیکدانان نظری برجسته بدنبال آن بودند می‌بایست نسبت به گذشته از گسترده‌گی و جامعیت بیشتری برخوردار باشد. برای چنین نظریه‌ای تنها کافی نبود که نور و گرانش را با یکدیگر پیوند دهد. در آن زمان محقق شده بود که بدون هیچ تردیدی کلیه پدیده‌های موجود در جهان، در بنیادیترین سطح خود، می‌توانند بوسیله چهار نیرو توصیف شوند. نیروی گرانش و نیروی الکترومغناطیسی دو تا از آنها بودند. نیروی الکترومغناطیسی، نیرویی جاذبه میان بارهای الکتریکی است که با نگاه داشتن الکترونهای دارای بار منفی در کنار هسته‌های دارای بار مثبت، موجب می‌شود تمام اتم‌ها درکنار یکدیگر قرار بگیرند. این نیرو همچنین باعث می‌شود تا در آهنربا قطبها همدیگر را جذب یا دفع کنند و یا برخی از فلزات جذب آن شوند. برخلاف اینکه به نظر می‌رسد نیروهای الکتریکی و مغناطیسی دو چیز کاملاً متفاوت هستند، باید به این نکته اشاره کنم که این تنها ظاهر قضیه است. مایکل فارادی در قرن نوزدهم نشان داد این دو نیرو بصورت بسیار نزدیکی با یکدیگر رابطه دارند و هر دو از همان نیروی الکترومغناطیسی منشاء می‌گیرند. تقریباً کلیه پدیده‌هایی که ما در اطراف خودمان مشاهده می‌کنیم بواسطه یکی از این دو نیرو هستند: گرانش و الکترومغناطیسی. ما اکنون می‌دانیم که علاوه بر دو نیروی مذکور، دو نیروی دیگر نیز وجود دارند که تنها در مقیاسهای کوچک عمل می‌کنند و محدود به هسته اتم هستند، ولی از نظر قوانین اصلی طبیعت، اهمیت آنها نیز به همان اندازه دو نیروی قبلی است [72].

بنابراین آن نظریه‌ نهایی که مدتها همه بدنبالش بودند و در آواخر دهه 1970 حاصل شد، نه فقط مانند نظریه کالوزا گرانش را با الکترومغناطیس پیوند می‌داد بلکه شامل دو نیروی هسته‌ای نیز بود. چنین نظریه‌ای را باید «نظریه همه چیز» نامید زیرا نشان می‌دهد که کلیه چهار نیروی طبیعت، تنها جنبه‌های مختلفِ یک « اَبَر نیروی» واحد هستند. دلیل اینکه نظریه کالوزا به صحنه بازگشت بدلیل روش زیرکانه‌ای بود که در آن بکار رفته بود و با اضافه کردن ابعاد بالاتر به معادلات، موجب یکپارچه شدن نیروی گرانش و الکترومغناطیس می‌شد. البته حالا که بجای دو نیرو، با چهار عدد از آنها سروکار داریم، ابعاد اضافی دیگری لازم است تا آنها نیز بصورت یک نیروی وحدت یافته درآیند. سرانجام در اواسط دهه 1980 نامزدی برای این نظریه‌ پیدا شد. این نظریه عنوان «نظریه اَبَر ریسمان‌ها» را گرفت و بسرعت به پرمایه‌ترین، برازنده‌ترین، پیچیده‌ترین، قدرتمندترین و مبهم‌ترین نظریه‌ای شده که تا کنون ابداع شده بود. بهرحال این نظریه‌ای بود که با ده بعد سروکار داشت، و اگر درست باشد، حاکی از این ‌است که ما در یک جهان ده‌- بُعدی زندگی می‌کنیم. ولی دراین‌حالت این شش بعد فضائی اضافی چنان بصورت یک کره شش بعدی بر روی خود جمع شده‌اند که قابل آشکارسازی (قابل دیدن) نیستند، و در این میان تنها همان چهار بعد فضازمانی باقی مانده است. از اینجهت به این نظریه نام اَبَر ریسمان داده‌اند زیرا حاکی از آن است که همه چیزها در کوچکترین سطح خود، از ریسمان‌هایی تشکیل شده‌اند که در این فضای ده بعدی در حال ارتعاش هستند. ممکن است غیرعاقلانه به‌نظر برسد، ولی حقیقتاً این نظریه توانسته است نسبیت عام را با مکانیک کوانتوم، که بهر حال برای فیزیک حالت جام مقدس [73] را دارد، یکپارچه سازد.

[1] - Stephen Hawking- (-1942) کیهان‌شناس معروف انگلیسی که در مورد فیزیک سیاه‌چاله‌ها تحقیقات بسیاری را انجام داده و از حدود سی سال پیش به بیماری ALS مبتلا بوده و بر روی صندلی چرخدار کارهای خود را دنبال می‌کند. (مترجم)

[2] - Terry Pratchett- (-1948) فانتزی نویس انگلیسی. (مترجم)

[3] - Star Trek - معروفترین، وشاید محبوب‌ترین سریال علمی- تخیلی که تا کنون ساخته شده. سری قدیمی این سریال در اوایل سال‌های دهه 50 شمسی از تلویزیون ایران با نام پیشتازان فضا پخش می‌شد. (مترجم)

[4] - Lewis Carroll (1898-1832) نویسنده انگلیسی. کتاب معروف او« آلیس در سرزمین عجایب» می‌باشد.« از درون آینه» ادامه داستان کتاب فوق است. (مترجم)

[5] - Common sense.

[6] - بطور دقیق دو تئوری نسبیت وجود دارد یکی تنوری نسبیت خاص (Special Relativity) و دیگری تئوری نسبیت عام (General Relativity).

[7] - بحثی که در فلسفه به نام جبر و اختیار معروف است. (مترجم)

[8] - D مخفف Dimension بمعنای بُعد است (مترجم)

[9] - Fred.

[10] - برای اینکه دقیقتر گفته باشم، هنگامی که در مورد خمیدگی فضای سه-بعدی صحبت میکنم، باید به جای آن دقیقتر بگویم خمیدگی «فضا زمان» چهار-بعدی. چیزی که نظریه نسبیت آینشتین به ما می‌گوید این ‌است که ترکیب فضای سه-بعدی و زمان، یک فضازمان چهار-بعدی را می‌سازد. ولی در حال حاضر من مبحث ترکیب فضا و زمان را به فصل‌های بعدی کتاب موکول می‌کنم.

[11] - Flatland.

[12] - Plainverse، در مقابل Universe به معنی جهان معمولی. (مترجم)

[13] - Open heart surgery عمل جراحی قلب که در آن سینه بیمار شکافته می‌شود. (مترجم)

[14] - من فرض می‌کنم که می‌توانیم با آنها صحبت کنیم و صدای آنها را نیز بشنویم. صدا بوسیله ارتعاش ملکولهای سه‌بعدی هوا تولید می‌شود. احتملاً این ارتعاشات می‌توانند به ملکولهای دو بعدی انتقال داده شوند و صدای مشابه‌ای تولید کنند. البته تمام این فرضیات کاملاً بیهوده است، ولی فکرکردن در مورد آن مایه تفریح خواهد بود.

[15] - مواقعی وجود دارد که مجموع زوایای مثلث رسم شده بر روی یک سطح خمیده از 180 درجه کمتر است. من بعداً به چنین خمیدگی‌هائی نیز اشاره خواهم کرد.

[16] - مدار شمالگان، مداری است به قطر حدود 250 کیلومتر که به همراه مدار استوا، مدار راس‌السرطان، مدار راس‌الجدی و مدار جنوبگان یکی از مدارهای مهم پنج گانه است. این مدار در 66 درجه و 34 دقیقه شمالی واقع شده است و مرز قاره قطب‌شمال را مشخص می‌کند. (مترجم)

[17] - radial direction.

[18] - Superstring Theory.

[19] - M-Theory . در اینجا M می‌تواند مخفف Mother (به معنی مادر) یا Membrane (به معنی پوسته) باشد. ولی نظریه-پوسته چنان نام ملال‌آوری است که بعضی از فیزیکدانان از آن به نام Magic-theory (نظریه – جادوئی) یاد می‌کنند زیرا عقیده دارند این نظریه می‌تواند همه نیروهای طبیعت را توضیح دهد.

[20] - نظریه ابر-ریسمان‌ها تعداد ابعاد فضایی را 9 و نظریه M تعداد ابعاد فضایی را 10 فرض می‌کنند.

[21] - Isaac Newton.

[22] - Woolsthorpe.

[23] - Lincolnshire.

[24] - Gottfried Leibnitz.

[25] - در زبان‌های لاتین «فیزیکی» به معنی جنسی/ جسمی نیز هست و این «فیزیکی» دوم بر همان مورد دلالت دارد. (مترجم)

[26] - البته در اساس وبا دستگاه‌هائی که بقدرکافی حساس باشند شما این توانائی را دارید که بگوئید اکنون کجا هستید، زیرا میدان جاذبه زمین به جای اینکه حالت صفحه‌ای داشته باشد حالت شعاعی دارد. یعنی اگر شما دو گوی را که باهم فاصله دارند به طرف زمین رها کنید، هر دو آنها در طول خطوطی حرکت خواهند کرد که آن خطوط به مرکز زمین می‌روند و این دوخط دقیقاً با هم موازی نیستند. در حالتی که سوار بر یک سفینه شتابدار باشید این دو خط کاملاً با هم موازی هستند.

[27] - اینکار در میان کسانی که خواهان هیجان زیاد هستند طرفدار دارد. (مترجم)

[28] - Cosmology.

[29] - ذرّات فرضی به نام تاکیون (Tachyon) در نسبیت خاص آینشتین پیش‌بینی شده‌اند که می‌توانند سریعتر از سرعت نور نیز حرکت کنند، ولی احتمالاً این نوع ذرّات در جهان واقعی وجود ندارند.

[30] - Beavis and Butthead- دو شخصیت خیالی در فیلم‌های انیمیشن MTV. این دو به خِنگ بودن، خبرابکاری و همچنین پرت و پلا گوئی معروف هستند. (مترجم)

[31] - Roald Dahl (1990-1916). نویسنده و فیلمنامه‌نویس انگلیسی. او بیشتر بخاطر داستانهایی فانتزی که برای بچه‌ها نوشته بود شهرت دارد. از جمله آثار معروف او چارلی و کارخانه شکلات سازی است، که در سال 2005 از روی آن فیلمی با همین عنوان و با شرکت جانی دِپ ساخته شده است. (مترجم)

[32] - David Bohm (1992-1917). فیزیکدان و فیلسوف شهیر آمریکایی که سهم مهمی در پیشبرد فیزیک نظری و بویژه فیزیک کوانتوم داشته است. (مترجم)

[33] - corpuscle.

[34] - Alien. یکی از معروفترین فیلم‌های ترسناک علمی تخیلی که بین سالهای 1979 و 1998 براساس آن چهار فیلم ساخته شده است. (مترجم)

[35] - diffraction.

[36] - James Clerk Maxwell.

[37] - Richard Feynman . (1988-1918)

[38] - در زبان انگلیسی عبارت «what is time?»، به دوصورت می‌تواند معنی شود: 1- «ساعت چنده؟» و یا «زمان چیست؟». اگر زمینه صحبت معلوم نباشد معنی مبهمی خواهد داشد. دراینجا معنی مورد نظر غریبه معنی شماره 1، و آن چیزی که رهگذر درک کرده، معنی شماره 2 است. (مترجم)

[39] - Gerald James Whitrow. (2000-1912) ریاضی‌دان، کیهان‌شناس و مورخ علم که کارهای زیادی در مورد مباحث فلسفی مربوط به زمان انجام داده بود. (مترجم)

[40] - بعبارت ساده‌تر ثانیه یعنی 86400/1یک روز، زیرا یک روز برابر است با 86400 = 24×60×60 ثانیه.

[41] - co-ordinated universal time.

[42] - دلیل عمده‌ای که باعث می‌شود بیشتر مردم نسبیت را فقط آن مباحثی بدانند که در نظریه نسبیت خاص مطرح می‌شود این ‌است که بواقع یادگرفتن نسبیت خاص از نسبیت عام آسانتر است، و درنتیجه خیلی‌ها با آن آشنا هستند. حتی ریاضیات بکارگرفته در این دو بسیار با هم متفاوتند. اگر کسی ریاضیات دوره دبیرستان را بداند، می‌تواند به جنبه‌های فنی نسبیت خاص وارد شود، ولی نسبیت عام به زمینه‌ها و ابزارهای ریاضی، همچون هندسه دیفرانسیل و حساب تانسوری، نیاز دارد که معمولاً در اواخر دوره‌های کارشناسی در رشته‌های فیزیک و ریاضی تدریس می‌شوند و در نتیجه تفسیر آنها دشوارتر می‌شود. ولی کلاً خواننده باید توجه داشته باشد که نسبیت خاص حالت خاصی از نظریه جامعتری بنام نسبیت عام است که گستردگی و جامعیت آن خیلی بیشتر است. (مترجم)

[43] - Lorentz transformation.

[44] - Thomas Young (1829-1773).

[45] - luminiferous ether.

[46] - closed timelike curves.

[47] - Kurt Gödel (1978-1906)، منطق‌دان، فیلسوف و یکی از ریاضیدانان برجسته قرن بیستم که در پیشبرد مبانی منطق و ریاضیات تلاشهای بسیاری را انجام داد. (مترجم)

[48] - Star Trek IV: The Voyage Home.

[49] - مهندس پرواز و یکی از افسران زیر دست فرمانده سفینه، کاپتان کِرک. (مترجم)

[50] - The Terminator paradox.

[51] - Arnold Schwartznegger (-1947). قهرمان سابق بدن‌سازی، هنرپیشه، بازرگان و سیاستمدار آمریکایی اطریشی‌تبار. در سال 2004 بعنوان فرماندار ایالت کالیفرنیا انتخاب شد. (مترجم)

[52] - Grandfather paradox.

[53] - John Fitzgerald Kennedy (1963-1917). سی‌وپنجمین رئیس جمهور آمریکا که در سال 1963 تررور شد. (مترجم)

[54] -Back to the Futhure.

[55] - billiard. یک بازی که با استفاده از چند توپ و برروی یک میز مخصوص انجام می‌شود. هدف بازی این ‌است که با استفاده از چوب مخصوص به یکی از توپها ضربه‌ای زده شود و آن توپ به بقیه خورده و موجب شود تا آنها بداخل سوراخ‌هایی که در اطراف میز قرار دارند بیفتند. (مترجم)

[56] - Carl Sagan (1996-1934)، ستاره شناس آمریکائی که سهم بسزائی در ساختن برنامه‌های علمی تلویزیونی برای عامه داشت. موضوع مورد علاقه او زیست شناسی فرا- ‌زمینی (exobiology) بود. تماس (Contact) تنها رومان او بود که بر اساس آن در سال 1997 فیلم موفقی به همین نام، به کارگردانی رابرت زِمِه‌کیس و با بازیگری جودی فاستر ساخته شد. (مترجم).

[57] - Matt Visser. ریاضی‌دان و کیهان‌شناس نیوزلندی که اکنون بعنوان یکی از متخصصین مطرح مبحث سیاه‌چاله‌ها و کرم‌چاله‌ها شناخته می‌شود. (مترجم)

[58] - Nathan Rosen (1995-1909).

[59] - Einstein Rosen Bridge.

[60] - Charles Dodgson (1898-1832).

[61] - antihorizon.

[62] - geometrodynamics.

[63] - Roy Kerr (-1934).

[64] - بنابراین مفهوم تکینگی‌ها از نقاطی با اندازه صفر بسیارکُلیتر هستند. یک تکینگی هرجایی است که مشخص کننده نوعی مرز در فضازمان است. بنابراین در مُدل فضای لاستیکی دو-بعدی، هر گونه بریدگی که در لاستیک بوجود می‌آید، یک تکینگی را تشکیل می‌دهد.

[65] - Willem Jacob van Stockum (1944-1910).

[66] - (Enterprise) سفینه فضایی خیالی در سریال تلویزیونی پیشتازان فضا. (مترجم)

[67] - یعنی یک جهان کلی یا فرضی. (مترجم)

[68] - C. P Snow (1980-1905). دانشمند و داستان‌نویس انگلیسی. کتاب دو فرهنگ دربردارنده مجموعه درسهای اوست که در سال 1959 درباره تفکیک و برخورد علوم خالص و علوم اجتماعی نوشته است. (مترجم)

[69] - Richard Feynman (1988-1918). فیزیکدان، نقاش و موسیقی‌دان آمریکائی. او یکی از پرنفوذترین فیزیکدانان معاصر بشمار می‌رود و برای کارهایی که در زمینه الکترودینامیک کوانتومی انجام داد، در سال 1965 برنده جایزه نوبل در رشته فیزیک شد. کتاب درسهایی از فیزیک، مجموعه درسهای او بود که در طول دهه 1960 در دانشگاه کالیفرنیا برای دانشجویان سالهای اول ارائه می‌داد و هنوز هم یکی از کتابهای درسی مطرح در این رشته محسوب می‌شود. (مترجم)

[70] - Theodor Kaluza (1954-1885).

[71] - Oskar Klein (1977-1894).

[72] - این دو نیرو یکی نیروی هسته‌ای قوی و دیگری نیروی هسته‌ای ضعیف می‌باشند، که همانطور که از نام آنها پیداست فقط در واکنش‌های هسته‌ای مطرح هستند. (مترجم)

[73] - جامی که حضرت عیسی در شام آخر خود از آن نوشید و از مقدس‌ترین نمادهای فرهنگ مسیحی بشمار می‌رود. (مترجم)

Like: ,

ترجمه‌های کامران بزرگزاد

show_banner(0);

سیاه‌چاله‌ها، کرم‌چاله‌ها و ماشین‌های زمان

نوشته جیم الخلیلی

ترجمه کامران بزرگزاد ایمانی

مقدمه مترجم

درباره کتاب

درباره نویسنده

اضافات مترجم

پیش‌گفتار

مقدمه

ده دقیقه کوتاه یا بلند؟

عقل سلیم (حواس معمول)[5]

بازگشت به آینده

با خودتان ملاقات کنید

فصل 1

بُعد چهارم

با اَشکال رابطه دارد

فضا چیست؟

جهان دو- بُعدی و موجودات دو- بُعدی

فضای خمیده

آیا واقعاً بُعد چهارمی در کار هست؟

فصل 2

اهمیت گرانش

سیب‌ و ماه‌

گرانش اینشتین

سقوط آزاد

فصل 3

جهان

آسمان شب

جهان چقدر بزرگ است؟

فصل 4

سیاه‌چاله‌ها

نور عجیب‌تر از آنیست که دیده می‌شود!

فصل 5

زمانه در حال تغییر است

زمان چیست؟

زمان را چه کسی ابداع کرده؟

فصل 6

زمان در نظریه اینشتین

چه چیز خاصی درمورد نسبیت خاص وجود دارد؟

دو چهره نور

فصل 7

پارادوکس سفردر زمان

پارادوکس تِرمی‌نِیتور[50]

فصل 8

کرم‌چاله‌ها

پلی بسوی جهانی دیگر

آلیس از درون آئینه

فصل 9

چگونه یک ماشین زمان بسازیم

حلقه‌های زمانی

فصل 10

چه می‌دانیم؟

نظریه همه چیز، مادر تمام ‌نظریه‌ها